三角形の面積の公式はどうして底辺×高さ÷2なのか？

三角形の面積は底辺 × 高さ ÷ 2で求めます。底辺が 6cm、高さが 4cm の三角形は 6 × 4 ÷ 2 = 12cm² になります。

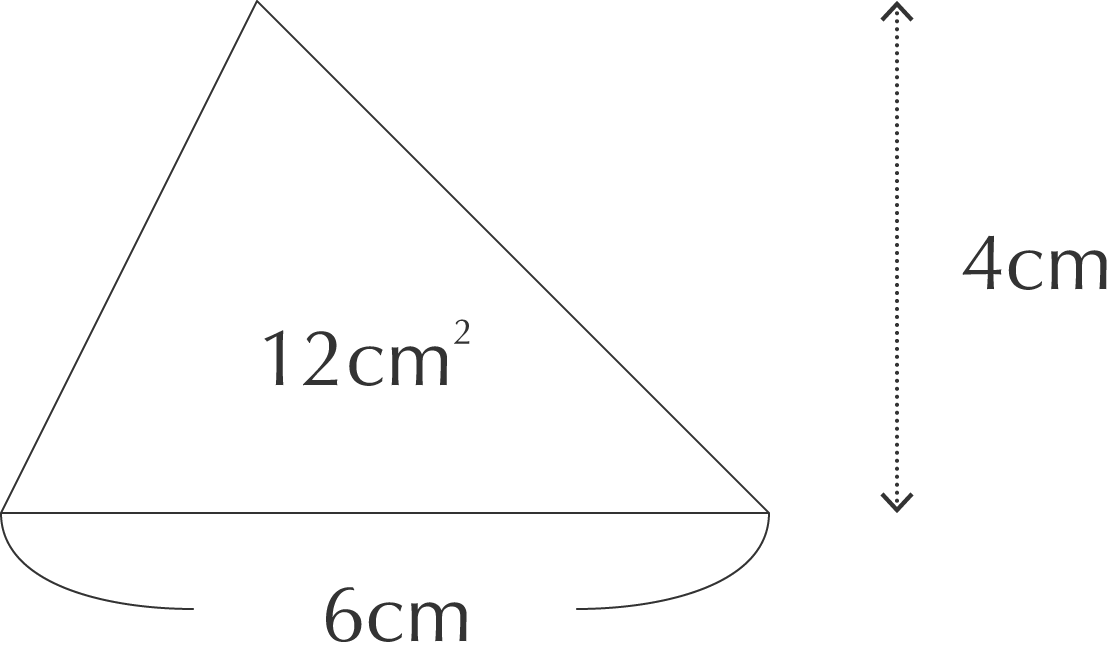
なぜ三角形の面積は底辺 × 高さ ÷ 2 で求められるのでしょうか？

直角三角形を考える

底辺が 6cm、高さが 4cm の直角三角形を考えてみます。

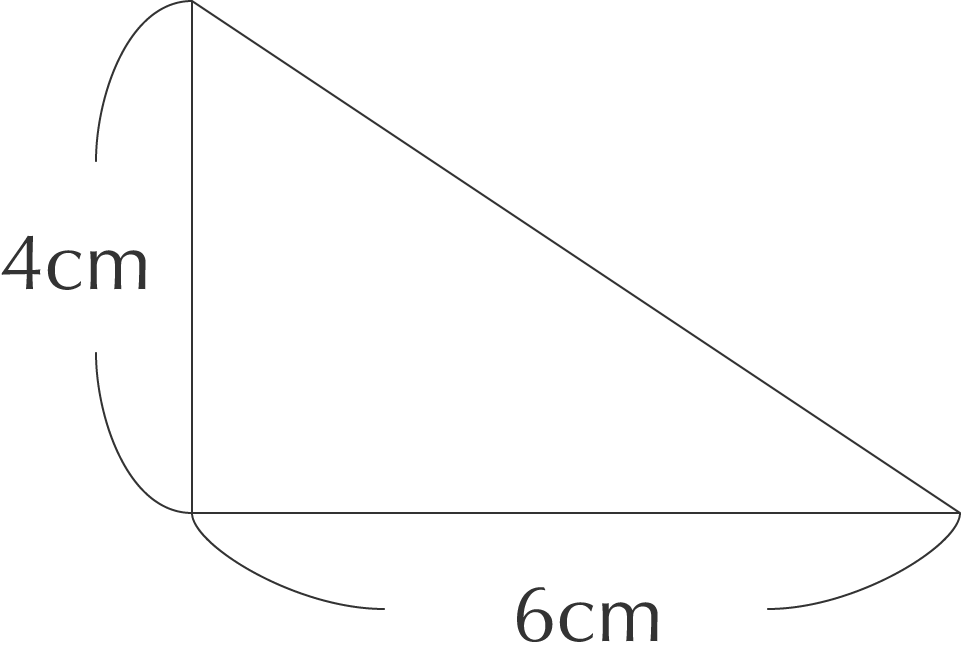
この三角形はたてが 4cm、よこが 6cm の長方形のちょうど半分です。

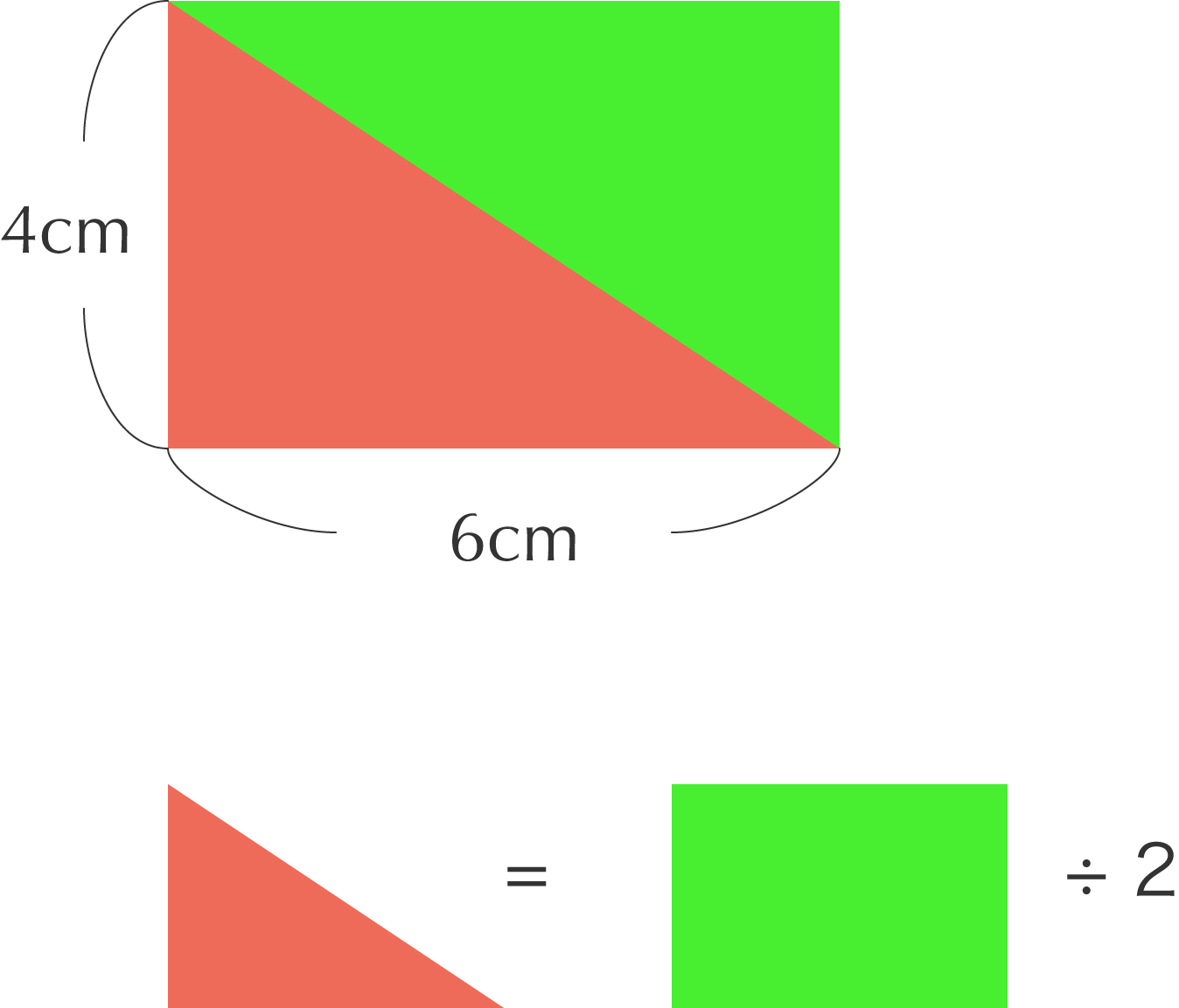
長方形は 4 × 6 = 24cm² なので、三角形は 24 ÷ 2 = 12cm² となります。

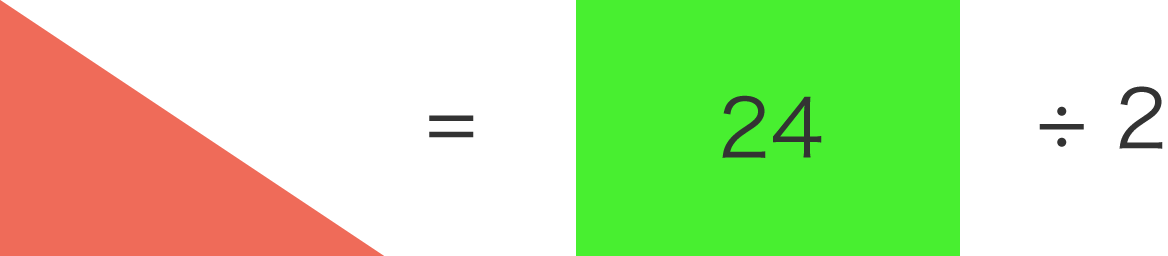
まとめると

4 × 6 ÷ 2 = 12

となり、底辺 × 高さ ÷ 2 の公式が出てきました。

ふつうの三角形

直角三角形ではない三角形はどのように考えるのでしょうか？

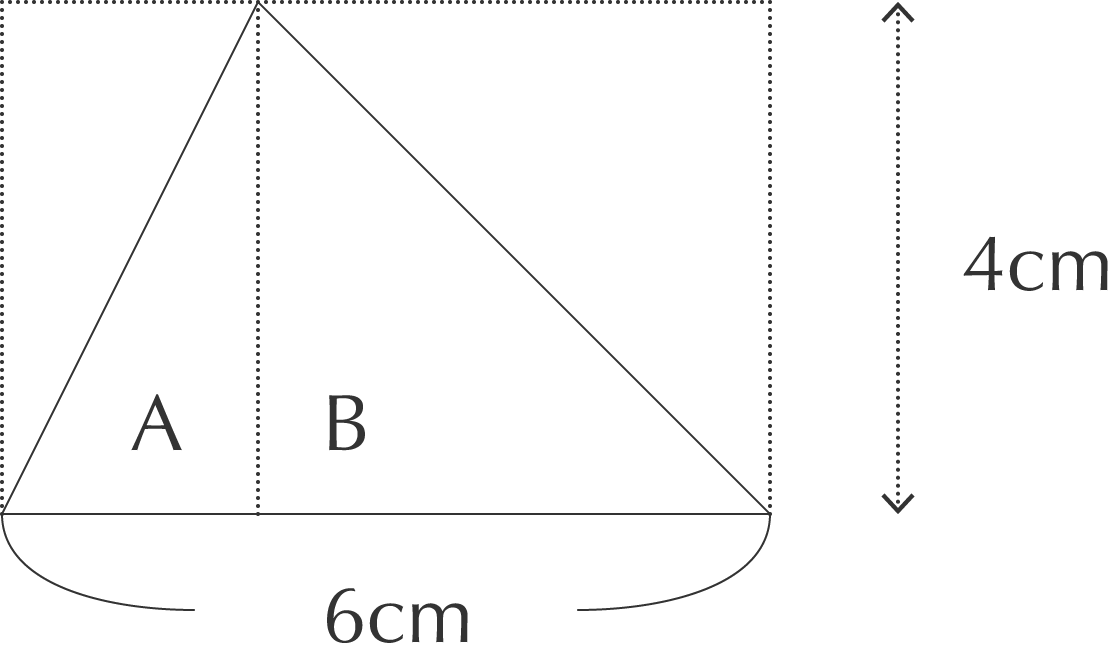
上図のように三角形を A と B に分けます。三角形は A + B となるわけです。たて 4cm、よこ 6cm の長方形は

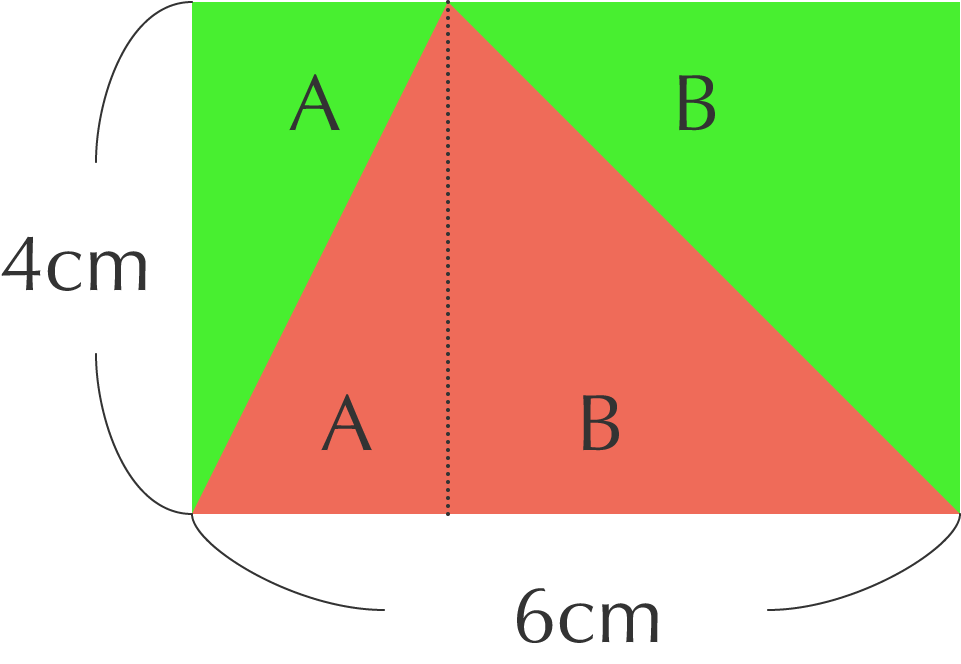
A が 2 つ、B が 2 つ合わさったものです。

長方形 = A + A + B + B

三角形 = A + B

三角形は長方形のちょうど半分だとわかります。以上から 24 ÷ 2 = 12cm² となります。

等積変形

底辺が 6cm、高さが 4cm であればどのような三角形も面積は 12cm² になります。

形が変わっても底辺と高さが同じであれば面積が同じになることを等積変形といいます。