のように という形の関数を一次関数といいます。次の関数はすべて一次関数です。
代入
は のとき となり、 のとき となります。
一次関数 の にいろいろな値を入れて と の関係を調べてみよう。
| x | y |
|---|---|
| -3 | -5 |
| -2 | -3 |
| -1 | -1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
座標
上の表で出てきた値を図にしてみよう。
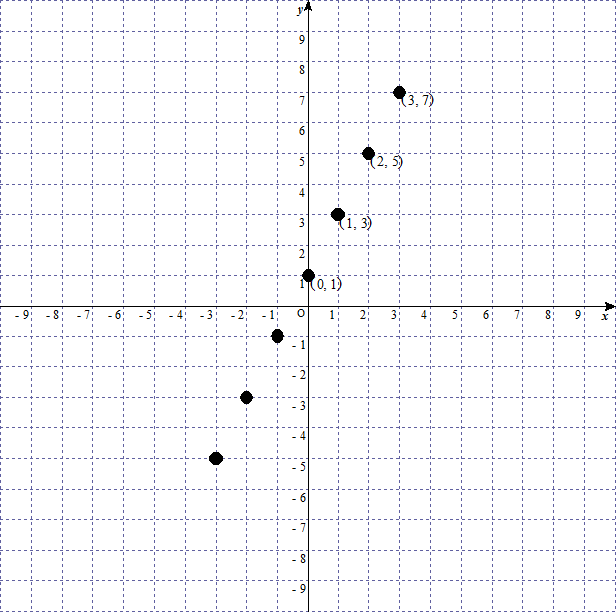
linear-function-graph-1
点を結び、線にする。
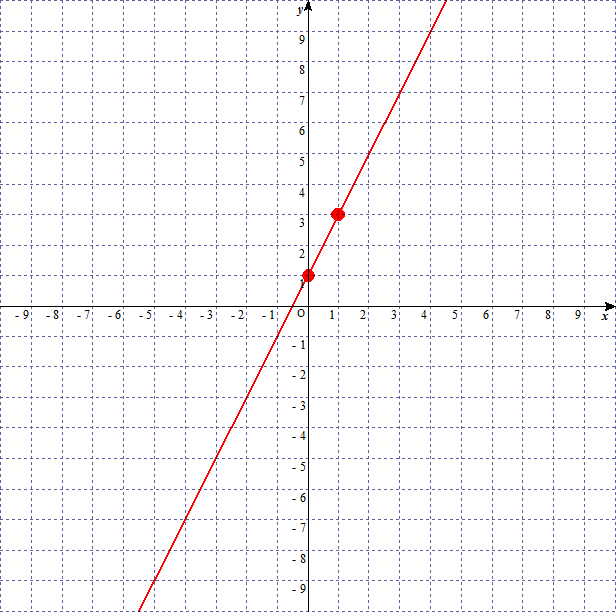
linear-function-graph-2
これを一次関数 のグラフという。一次関数のグラフは二つのポイントがあります。
- 一次関数のグラフは直線
- 二つの点がわかればグラフがわかる
上の赤い直線も と の二点を結んでいる。
グラフの書き方(基本)
を書いてみよう。二つの点がわかればグラフがわかるので、二つの点を適当に求める。
例えば に と を入れると
| x | y |
|---|---|
| 1 | 1 |
| 2 | 4 |
となる。つまりこのグラフは と の二点を通ります。
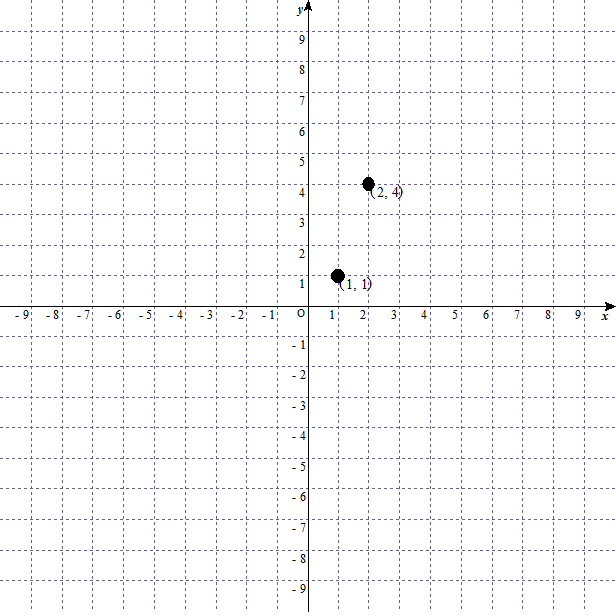
linear-function-graph-3
この二点を結ぶと、 のグラフになる。
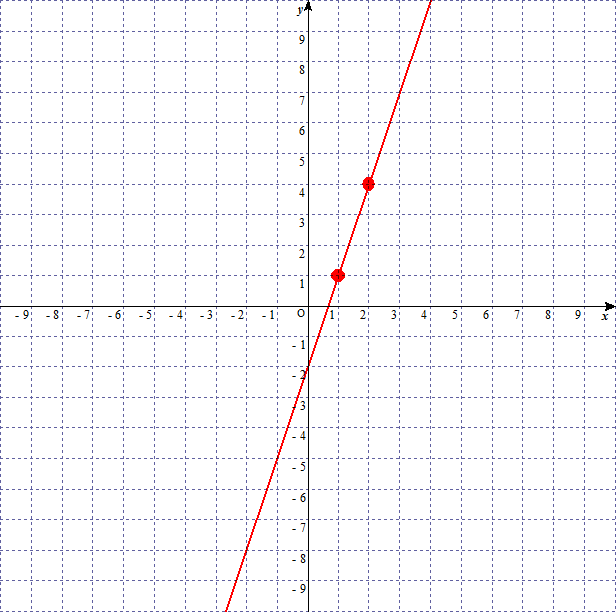
linear-function-graph-4
一次関数のグラフの簡単な書き方(応用)
という一次関数のグラフを書いてみよう。前問と同じように二つの点を求めますが、なるべく の値が整数になるようにします。例えば に を入れてしまうと
となってしまい、座標に点をプロットしにくくなってしまう。 という点を無理にとったらグラフは不正確になってしまうかも。そこで としてみる。この は の分母の です。
きれいな数になった。つまりこのグラフは を通ります。グラフを書くにはあともう一つの点が必要ですが、ここでは をとってみよう。
やはりきれいな数になった。整理すると
となります。このグラフは と の二点を通る。
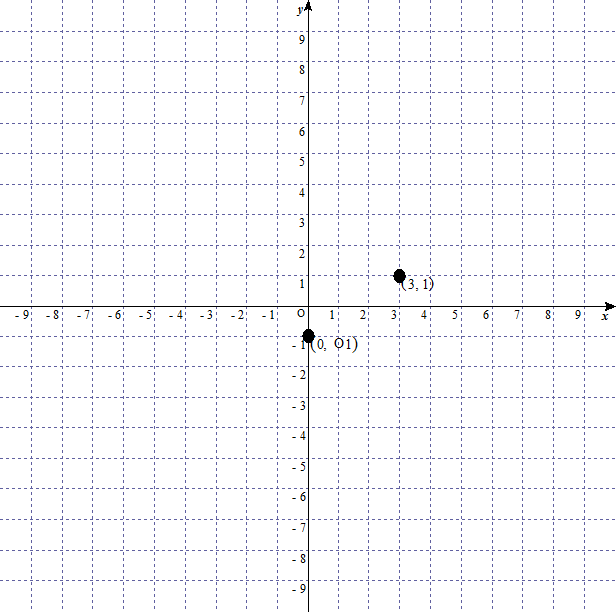
linear-function-graph-5
二点を結ぶと
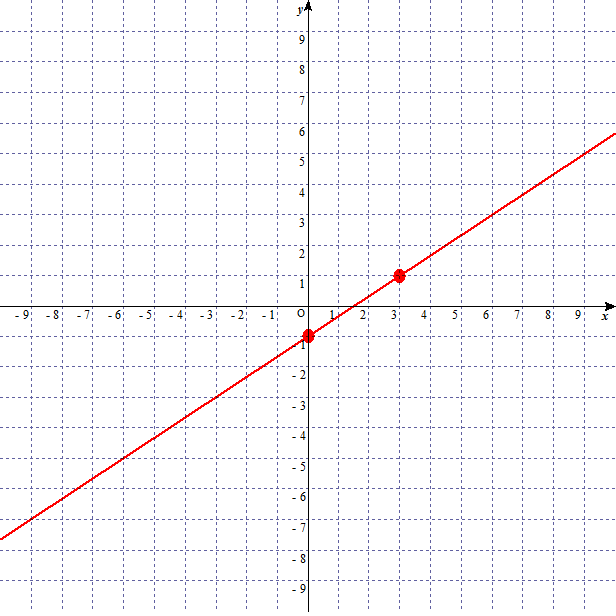
linear-function-graph-6
グラフが完成する。
切片
直線のグラフと 軸の交点の座標を切片といいます。例えば

linear-function-graph-2
の切片は、グラフと 軸が で交わっているから です。グラフの切片は の に等しい。
の切片は
の切片は
の切片は
…
本当に合っているか確かめよう。 と と のグラフは
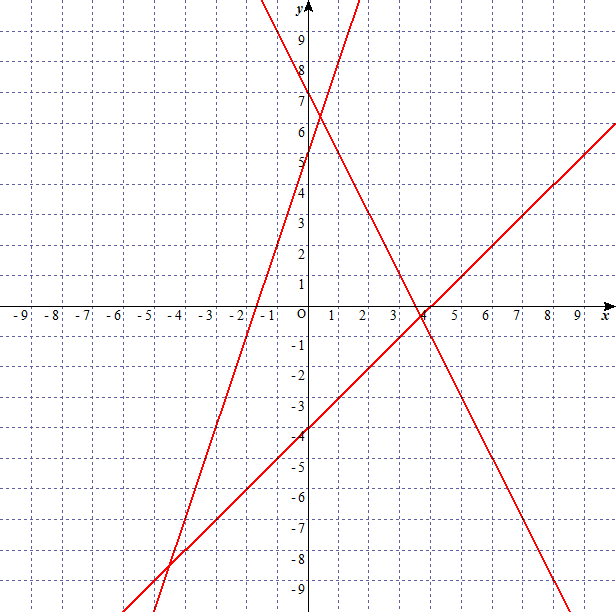
linear-function-graph-8
となるため、切片が合っていることがわかる。
傾き
次の三つのグラフを考える。
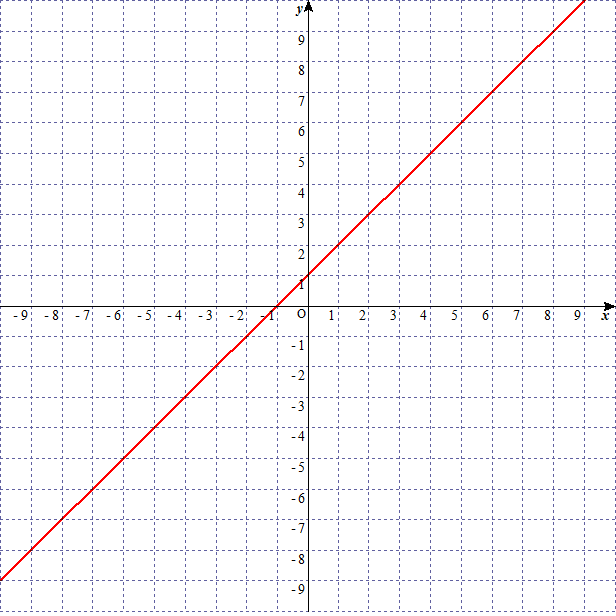
linear-function-graph-10-a
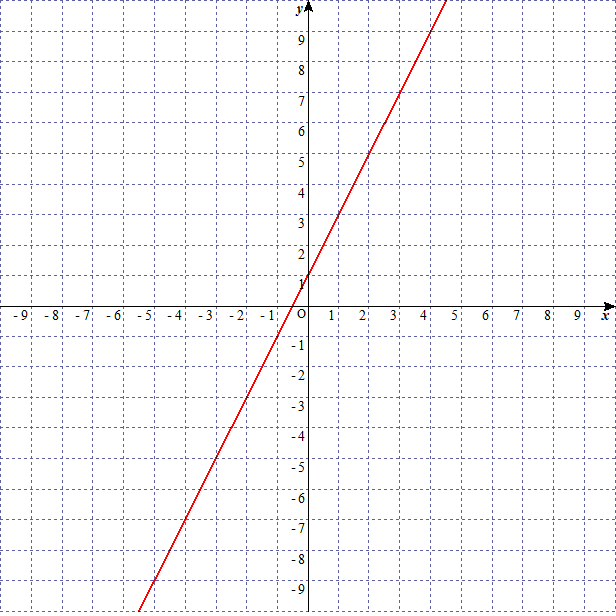
linear-function-graph-10-b
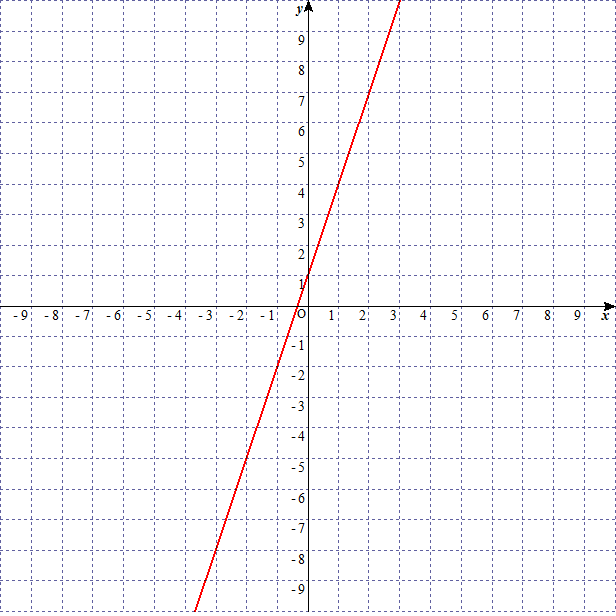
linear-function-graph-10-c
の が大きくなればなるほど、グラフの傾きが急になっていることがわかります。このことから の を傾きという。
例えば
の傾きは
の傾きは
の傾きは
…
です。







