円すい（円錐）の体積の求め方と問題｜小学数学
円すい（円錐）の体積は
底面積 × 高さ ÷ 3
で求まります。例えば、底面が半径 4cm の円、高さが 6cm の円すいの体積を求めてみよう。
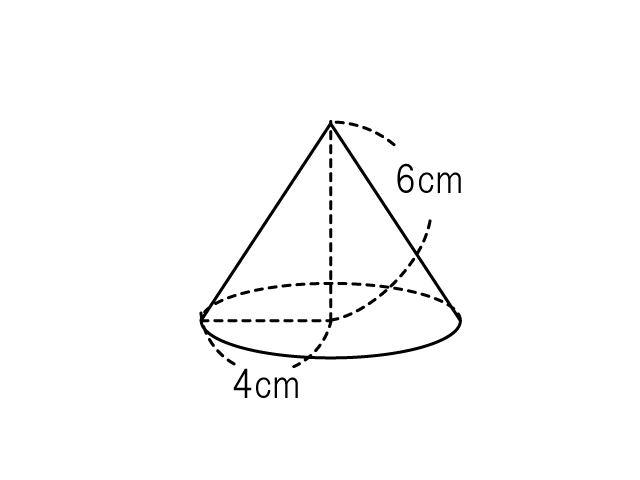
calculation_cone_1
底面積 = 4 × 4 × 3.14
高さ = 6
体積 = 4 × 4 × 3.14 × 6 ÷ 3
= 4 × 4 × 3.14 × 2
= 100.48
体積は 100.48cm² となります。体積を求めるときは、面積を計算する前に体積の式をつくります。円周率 3.14 の計算はなるべく一度ですませましょう。よく出る計算は下の記事で紹介しています。
円周率（3.14）のかけ算（3.14×1から3.14×128まで）
底面が半径 3cm の円、高さが 4cm の円すいの体積
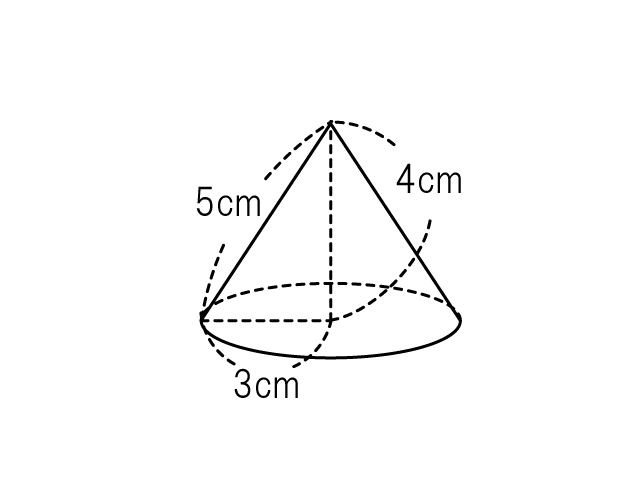
calculation_cone_2
底面積 = 3 × 3 × 3.14
高さ = 4
体積 = 3 × 3 × 3.14 × 4 ÷ 3
= 3 × 4 × 3.14
= 37.68
体積は 37.68cm² となります。
底面が半径 5cm の円、高さが 12cm の円すいの体積
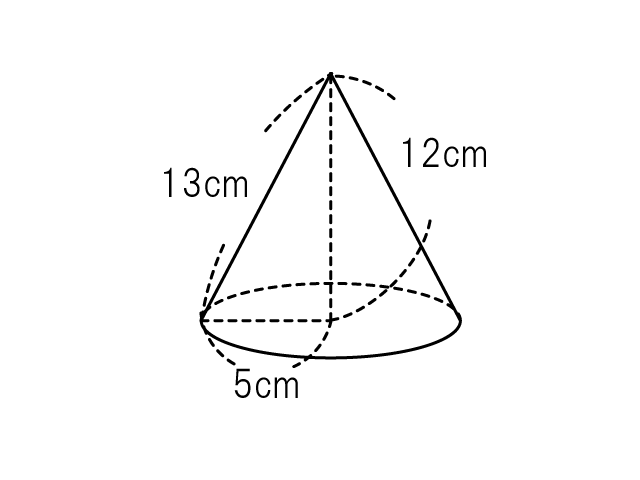
calculation_cone_3
底面積 = 5 × 5 × 3.14
高さ = 12
体積 = 5 × 5 × 3.14 × 12 ÷ 3
= 5 × 5 × 3.14 × 4
= 100 × 3.14
= 314
体積は 314cm² となります。
円すいの体積を求めるときに必要なもの
- 計算の工夫ができる
- 前から順番に計算するのでなく、割り算を最初に計算するといった応用力がある
- 円周率のかけ算をある程度覚えている
円すいの体積に限らず、図形の面積や体積の問題は計算の工夫にポイントがあります。公式を知っている人は解けます。でもみんながみんな満点をとるわけではない。それは計算の工夫ができるか、できないかで決まります。
例を見てください。先ほどの円すいで出てきた式です。
5 × 5 × 3.14 × 12 ÷ 3
= 5 × 5 × 3.14 × 4
最初に 12 ÷ 3 をやって 4 を求めています。そして 5 × 5 × 3.14 を計算する前に 5 × 5 × 4 = 100 を計算する。そうすれば 3.14 × 100 という単純な式にもっていける。
