中学受験の算数でマッチを使った問題はよく出てきますね。マッチをつなげて正三角形や正方形を作る。何個できるか？という問題です。
中でも「マッチ6本で正三角形を4つ作るには、マッチをどうつなげればいいか？」という問題。答えはわかりますか？
マッチ3本で正三角形は1個できる
三角形を作るにはマッチ3本が必要で、単純に考えれば4×3=12本のマッチが答えになりそうです。でも12本が多いことはなんとなくわかりますよね。むしろ12本という数は最大値です。
この問題、こうしたパズル的な問題を解くには、普段からさまざまな知識を入れていることが不可欠です。正四面体の面と線の数はそれぞれいくつありますか？
正四面体の面は4つ、線は6つ
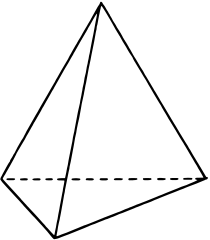
上の正四面体を見てください。同じ正方形が4つ合わさったものを正四面体といいましたね。面の数はもちろん4つ、そして線の数は6本です！
この正四面体の線をマッチ棒に置き換えれば、マッチ6本で正三角形が4つできることがわかります。つまりこの問題の答えは「正四面体」となります。
正四面体のまとめ
正四面体
面の数 4
線の数 6
この数たちはよく覚えておきましょう。正四面体は算数と数学で最もよく出てくる図形の一つです。
