A:Bに対してB:Aを逆比といいます。例えば2:3の逆比は3:2になります。
逆比そのものは比をひっくり返すだけで計算できますが、どうして逆比というものを考える必要があるのでしょうか?
長さと面積
AとBという同じ面積の長方形があり、Aの横の長さとBの横の長さは3:4だとします。このときAの縦の長さとBの縦の長さの比はいくつでしょうか?
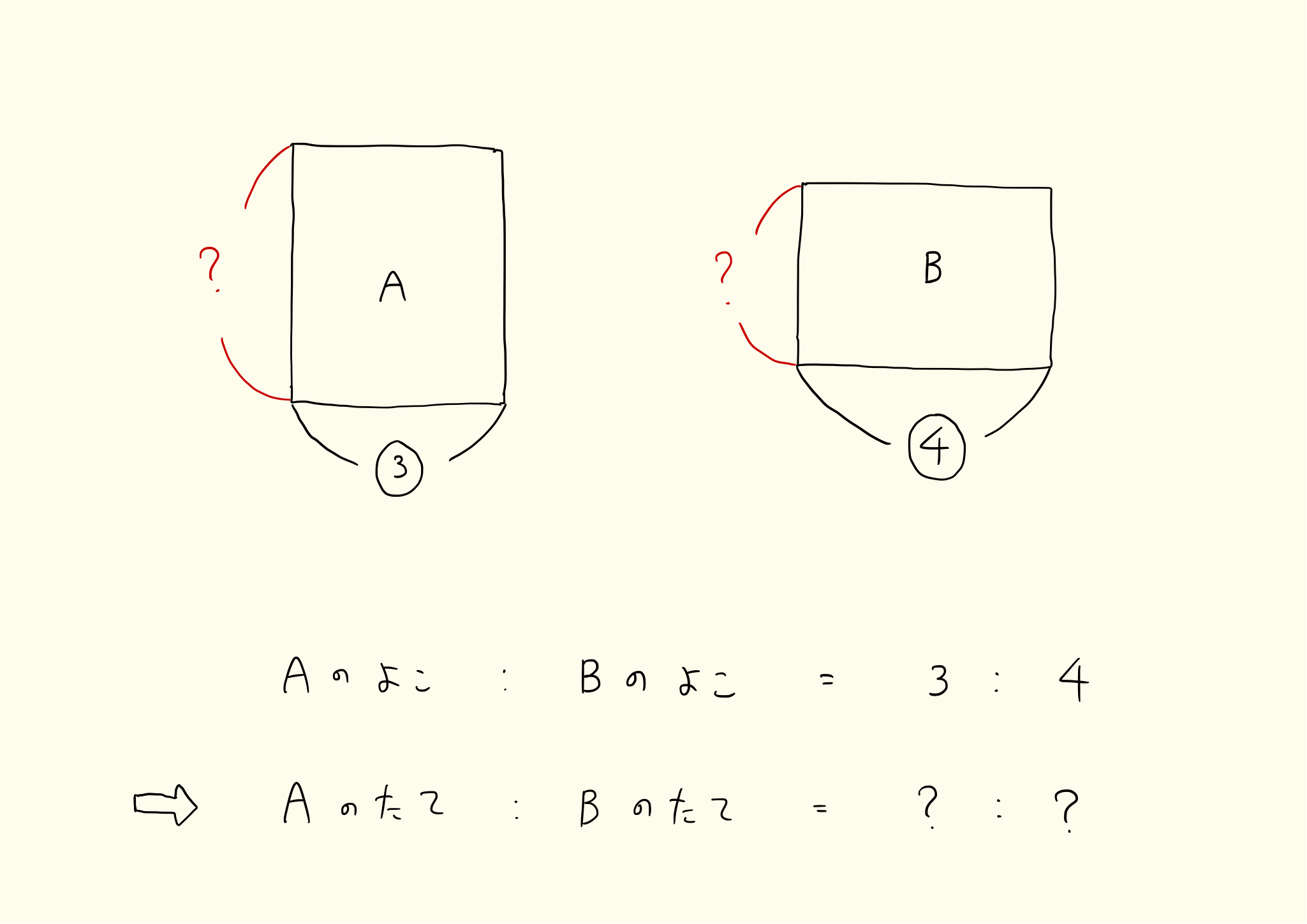
ratio_inverse_1
このような問題を考えるとき、逆比が役に立ちます。AとBの面積が同じなので、どちらの面積も12だとしましょう。本当は12ではないかもしれませんが、今は12だとします。
すると
Aの縦=12÷3=4
Bの縦=12÷4=3
となり、Aの縦の長さとBの縦の長さは4:3となりました。これは横の3:4をひっくり返したものです。つまり縦の比は横の比の逆比であることがわかりました。
例題
次の比の逆比を求めなさい。
(1)3:4
(2)7:2
(3)12:8
(4)2:10
解答
2つの比の逆比は、その2つの数をひっくり返すだけです。
(1)4:3
(2)2:7
(3)8:12=2:3
(4)10:2=5:1
小数の比
0.25:0.4のような比の逆比はどのようになるでしょうか? まずは2つの数をひっくり返して0.4:0.25として、次に0.4と0.25をそれぞれ100倍して40と25にします。
0.4:0.25
=40:25
=8:5
分数の比
2/3:1/4といった分数の比も、逆比を求めるときは2つの数をひっくり返します。
1/4:2/3
分母に注目して、通分するように4と3を12にそろえます。
1/4:2/3
=3/12:8/12
分子だけをとりだして
3:8
となります。
3つ以上の比
3:4:6といった3つの数の比は、それらの数の最小公倍数をまずは計算します。この場合は12です。
(3,4,6)=12
この最小公倍数で3つの数を割ります。
3→4
4→3
6→2
割ってでてきた数を並べた4:3:2がもとの比の逆比になります。
逆比の本当の定義
最初に逆比は「比をひっくり返した比」といいました。2つの比(○:△のような比)のときはひっくり返すだけですが、3つの比のときは計算が複雑になってしまいました。
逆比は、本当は次のように考えます。
a:b
→1/a:1/b
順番をひっくり返すのでなく、値を1で割った値を並べます。これを逆比といいます。例えば3:4の逆比は
1/3:1/4
となります。しかし分数の比はとてもわかりにくいため、結局左右に12をかけて
1/3:1/4
=4:3
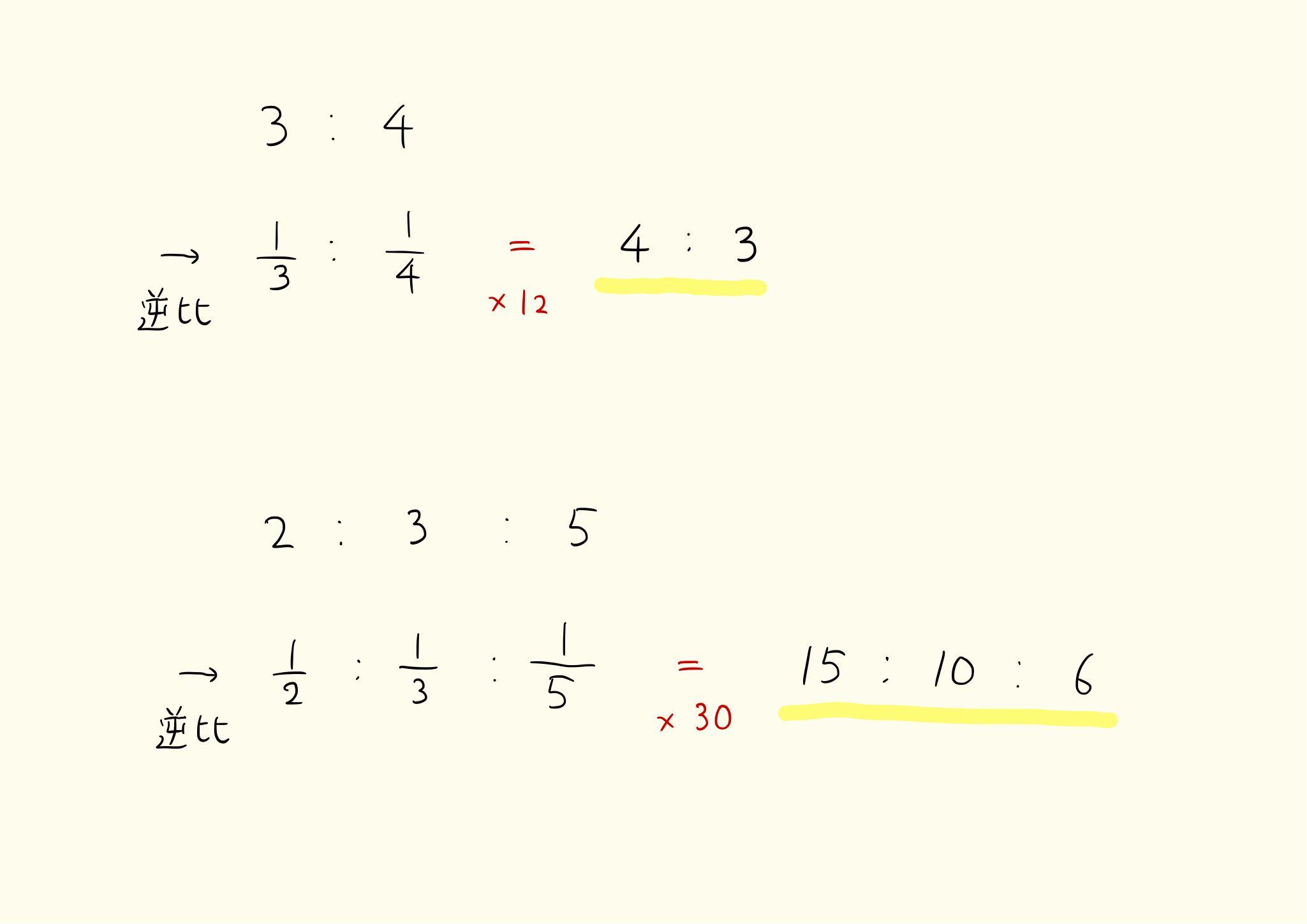
ratio_inverse_2
とします。3:4の逆比は4:3だとわかりました。これは順番をひっくり返した比となっています。






