積分は微分の逆です。微分した関数を積分すると元に戻り、積分した関数を微分すると元に戻ります。
不定積分
積分は微分の反対です。x^2を微分すると2xになり、2xを積分するとx^2になります。○を積分した関数は、その関数を微分して○になる関数です。

integral_1
下図を見てください。定数を積分すると一次関数、一次関数を積分すると二次関数、99次関数を積分すると100次関数になっています。赤字で書かれている公式のとおり、x^nを積分すると係数はn+1の逆数になります。積分するときは係数の計算が大変です。
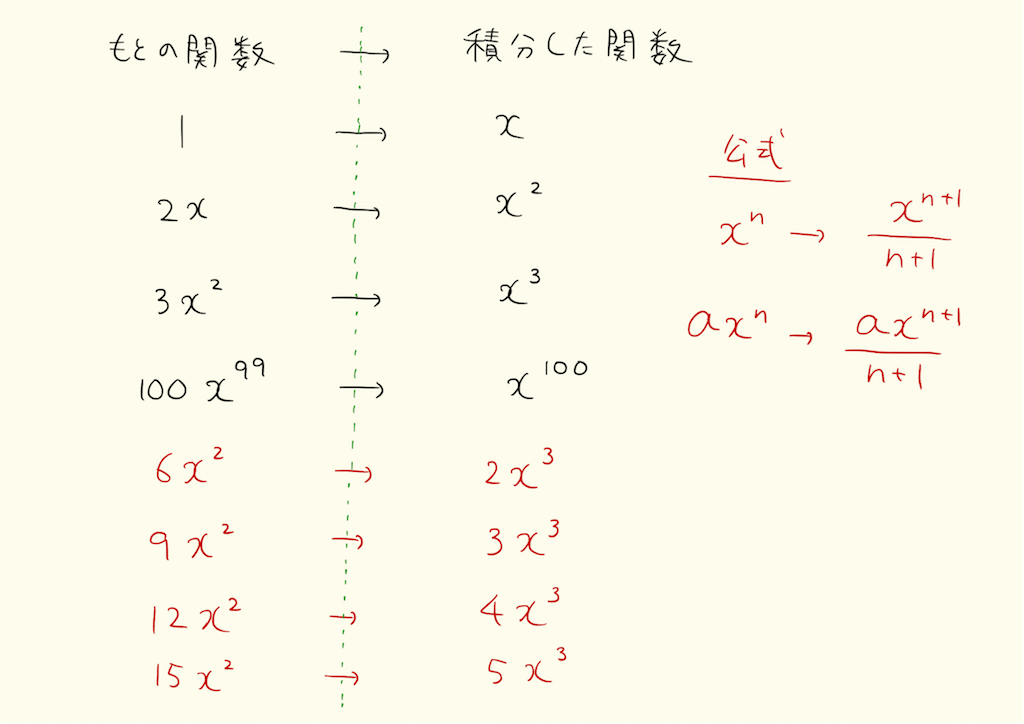
integral_2
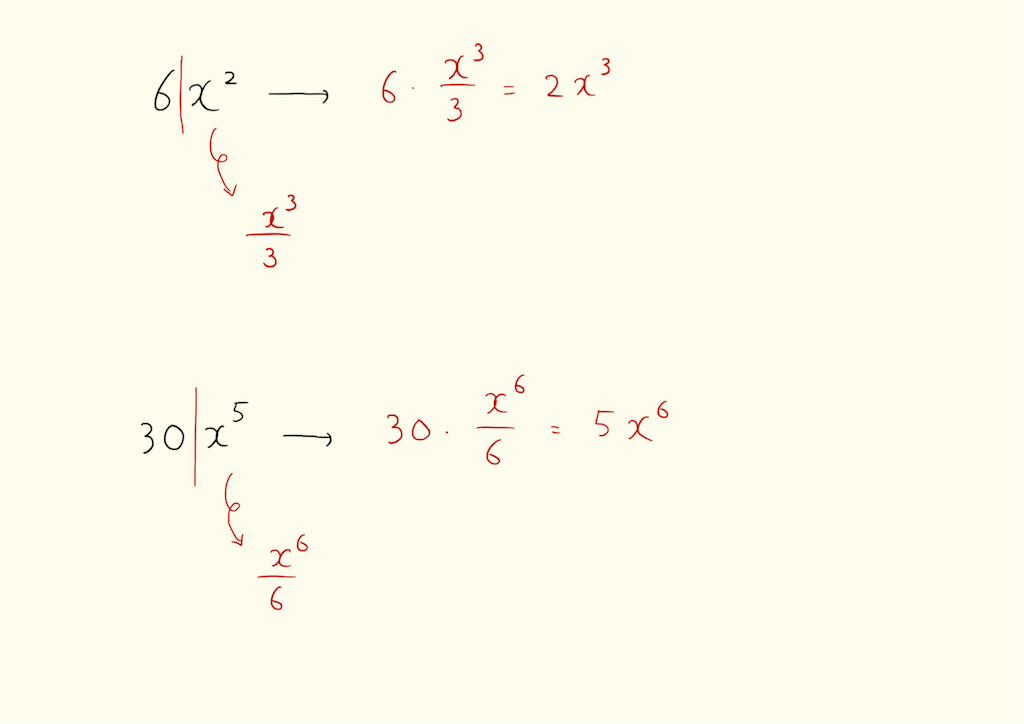
integral_3
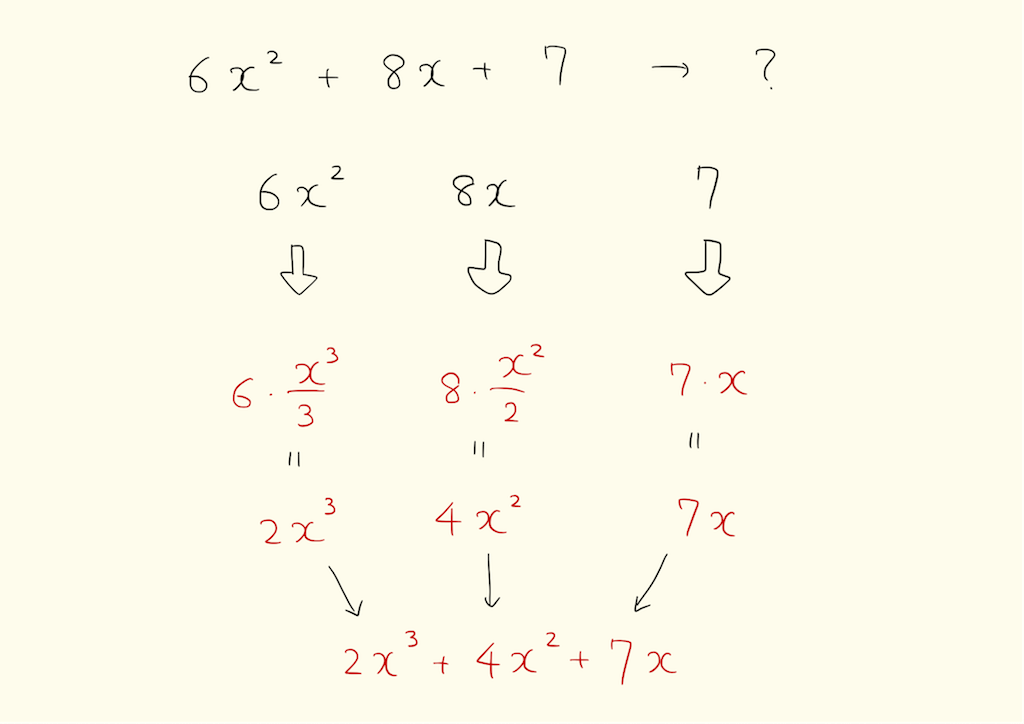
x^nの積分がわかったら、続いて多項式の積分を計算しましょう。それぞれの項を積分して後で足すだけです。
integral_4

integral_5
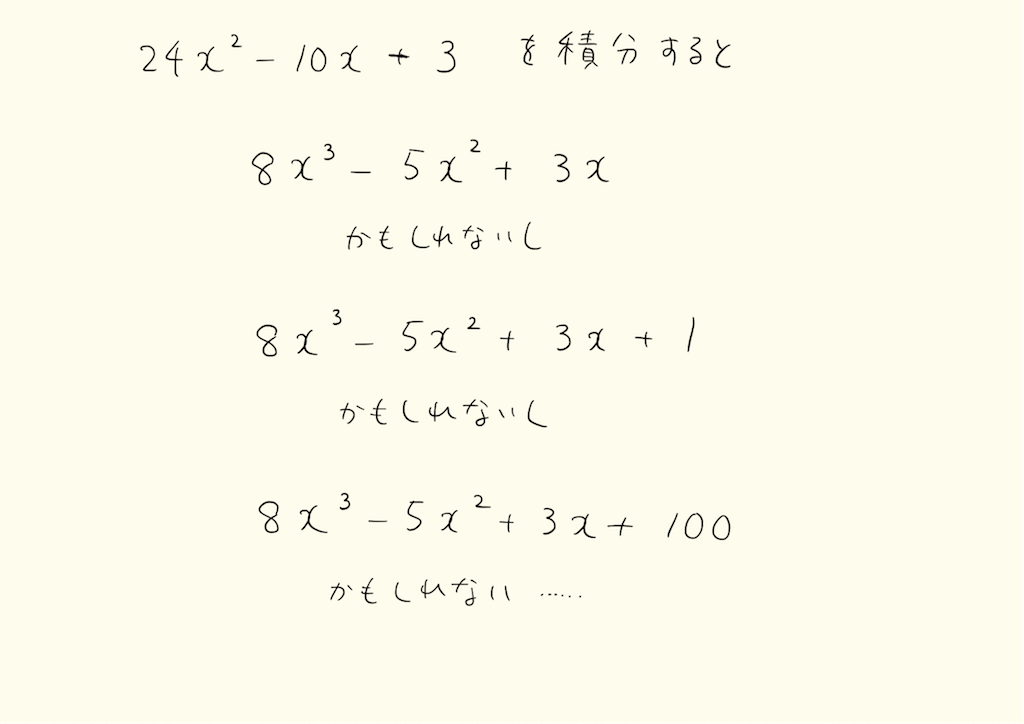
integral_6

integral_7
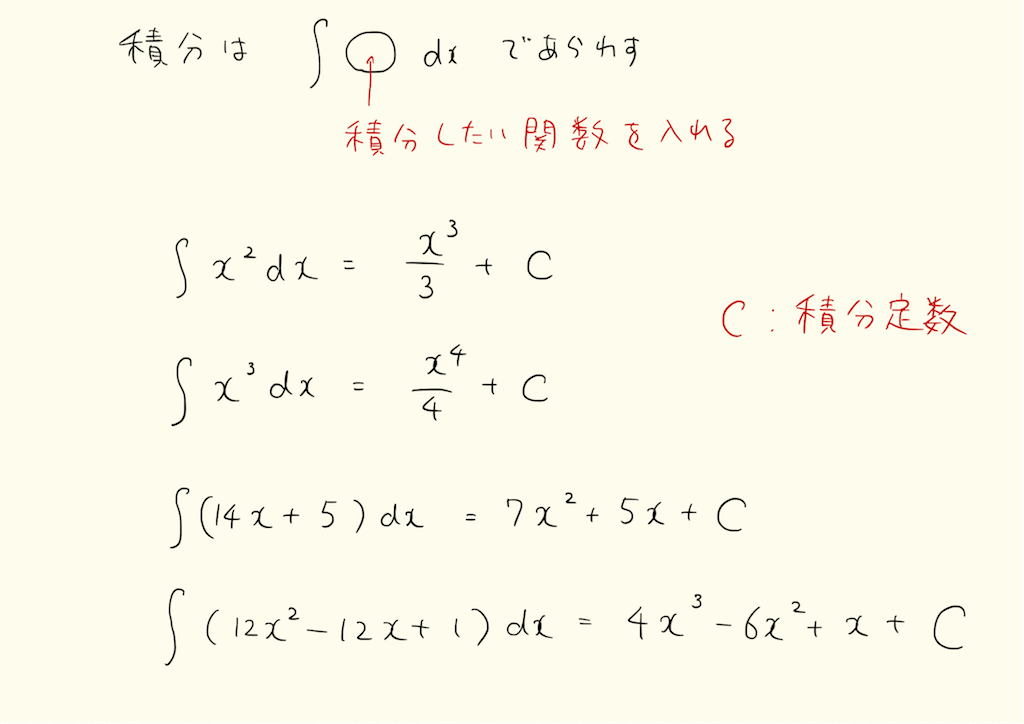
integral_8
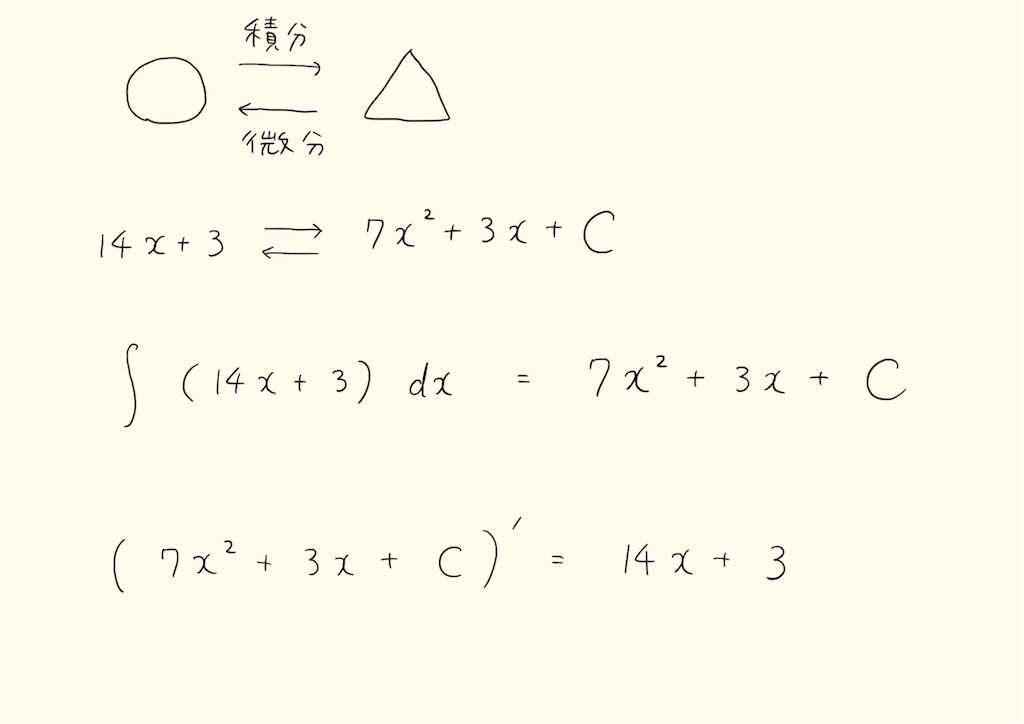
integral_9
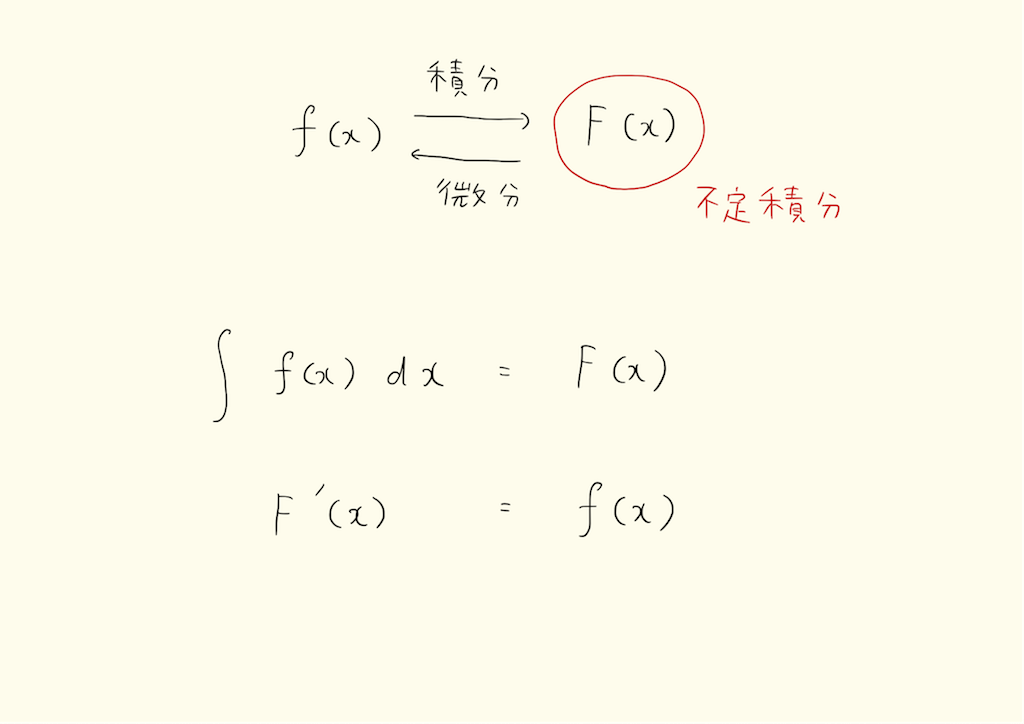
integral_10
定積分
積分記号の上下に数字が添えられた積分を定積分といいます。これは積分したい範囲を指定するときに使います。不定積分すると関数が出てきますが、定積分は値が出てきます。

integral_11
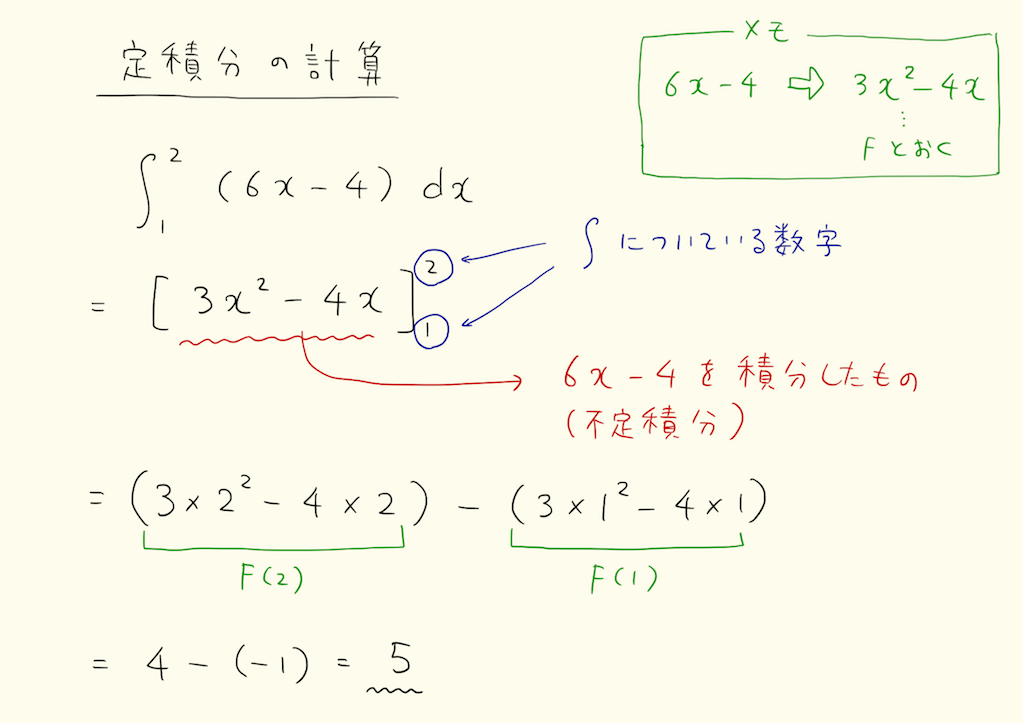
不定積分のxにaとbを代入したF(a)とF(b)の差を定積分とする。不定積分は関数、定積分は値になることに注意しよう。上下の添字がないと定積分は計算できない。
例えば10x+3を7から9まで積分すると166になる。
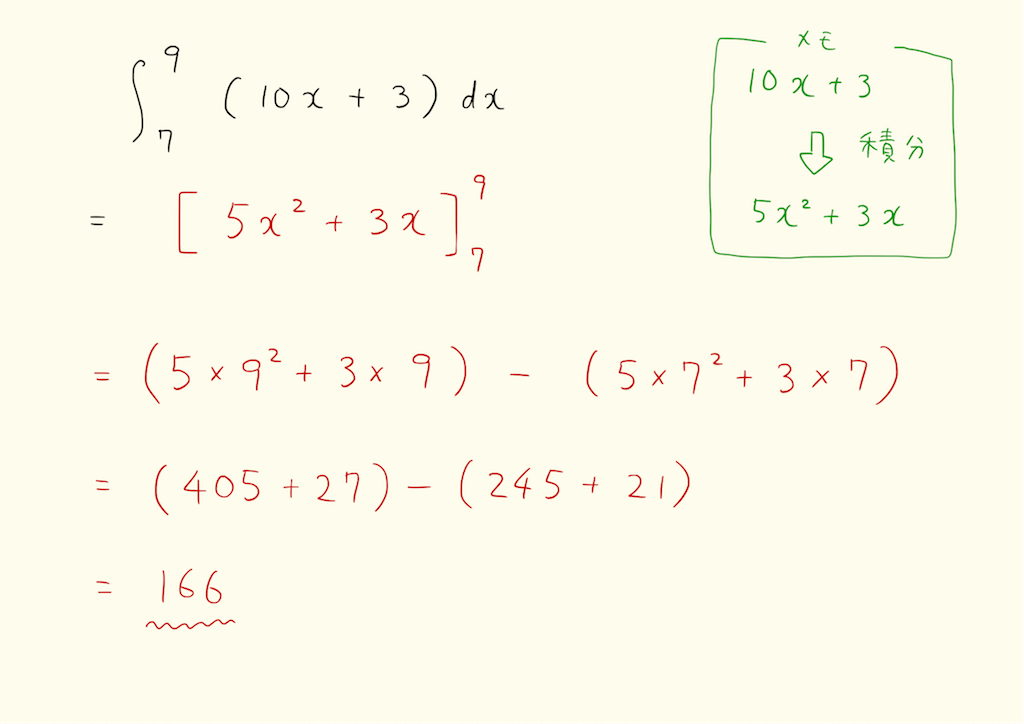
integral_12
integral_13
定積分は不定積分が土台になっているため、正しい定積分の値を求めるときは不定積分が正しいかきちんと確かめよう。
面積
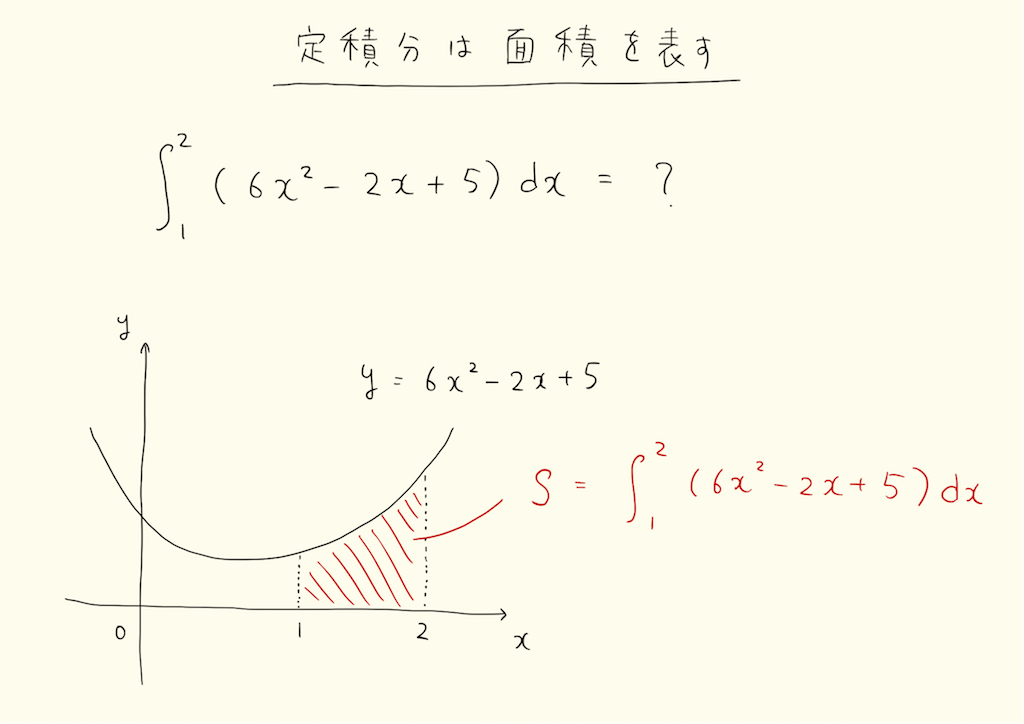
定積分は、関数とx軸にはさまれた領域の面積を表します。もしxを時間、yを速度としたら、関数とx軸にはさまれた部分は距離になります。
integral_14
追記中…









