微分は関数の変化率を求めるものです。変化率(特に平均変化率)は
の変化量 ÷ の変化量
です。
を時間、 を距離と考えると変化率は速度を表します。変化率が大きいとき、 が少し変化するだけで は大きく変化します。
平均変化率
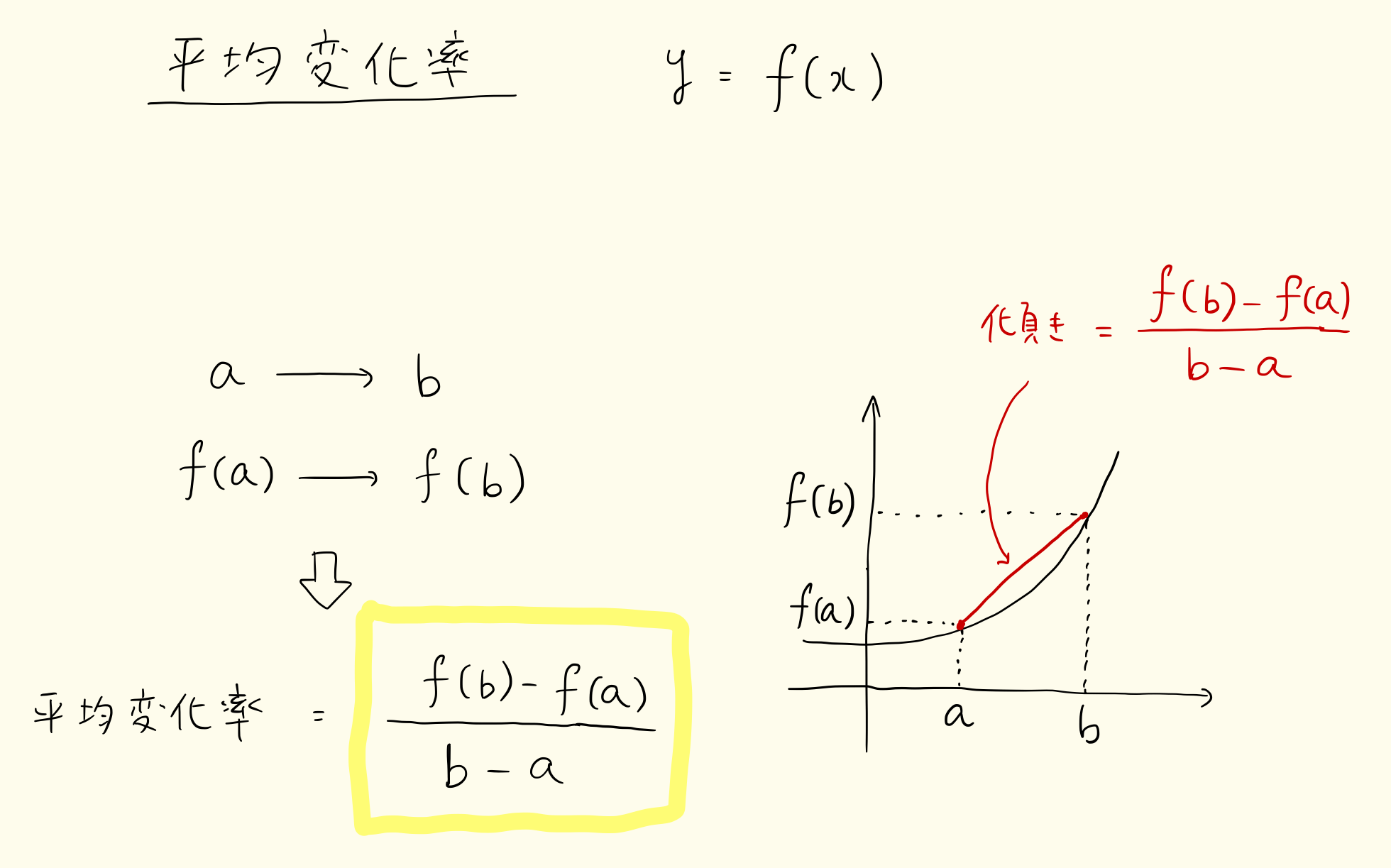
無題の画像
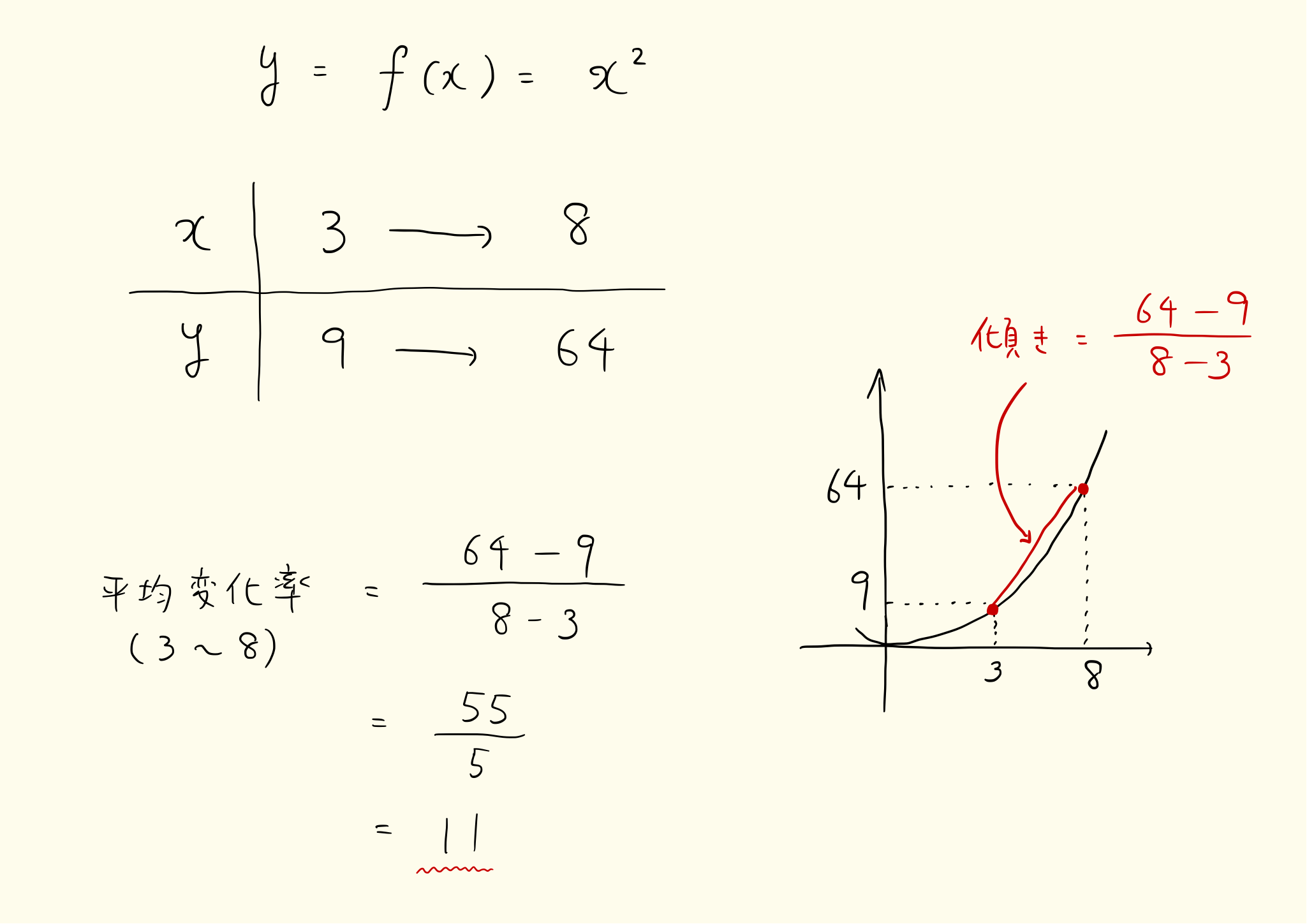
無題の画像
グラフの抽象的な理解
下図のように b 点を a 点に近づけると、平均変化率は a での変化率に近づきます。
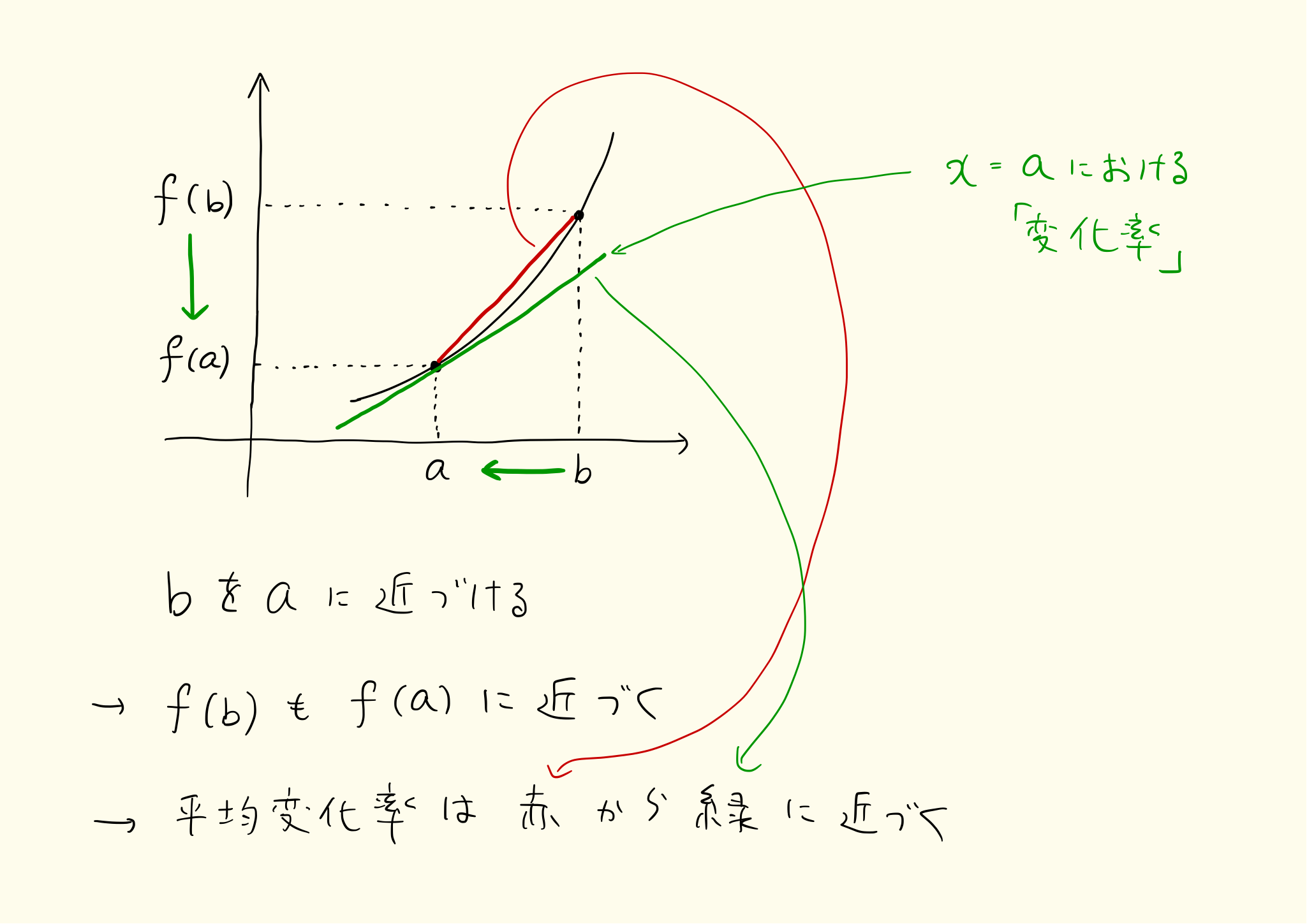
derivative_3
b と a が遠いと、a から b までの平均変化率は大雑把な値になります。a と b の間隔を短くすれば、平均変化率の「精度」が上がって、ついには a 地点での変化率になる。
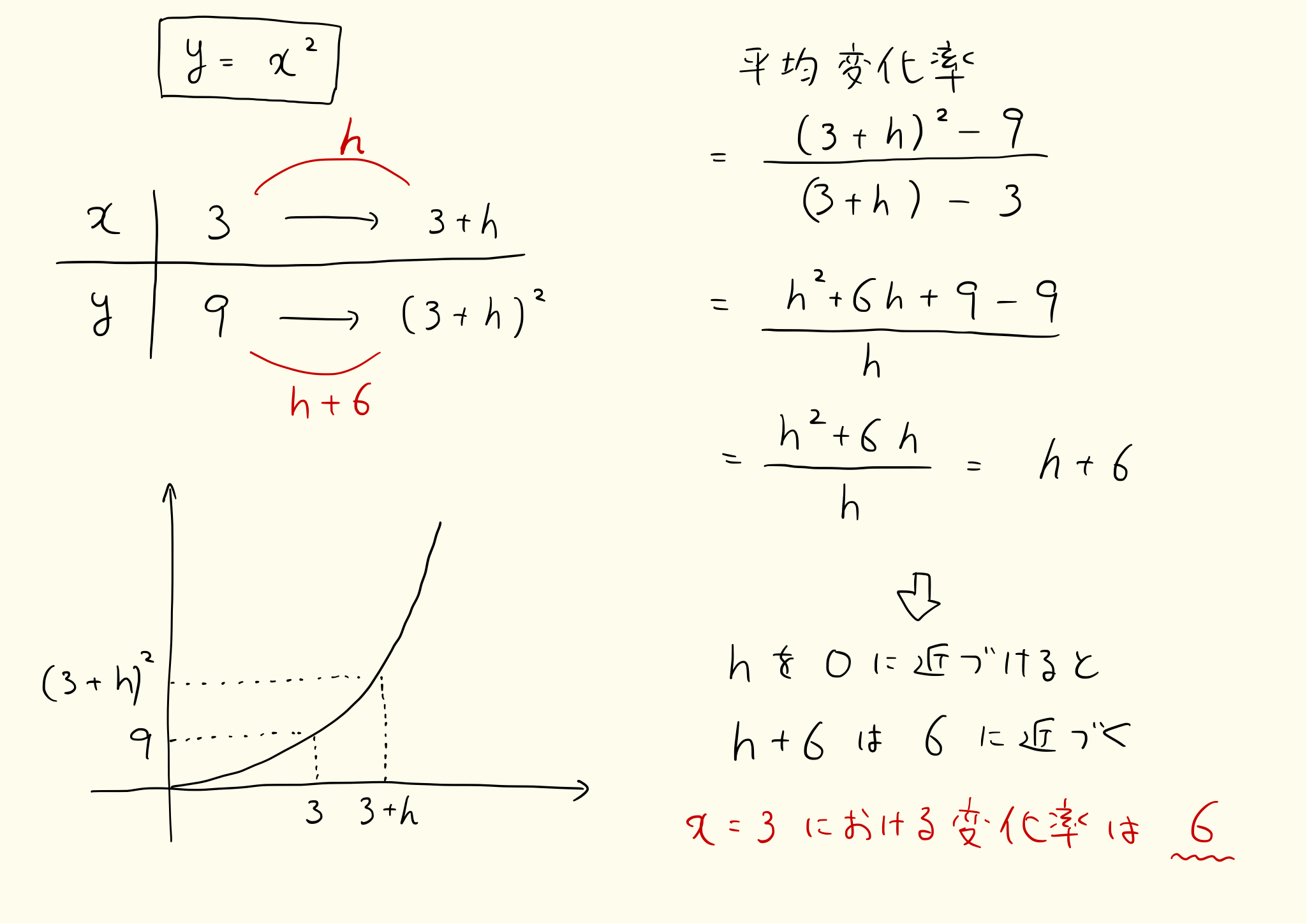
derivative_4
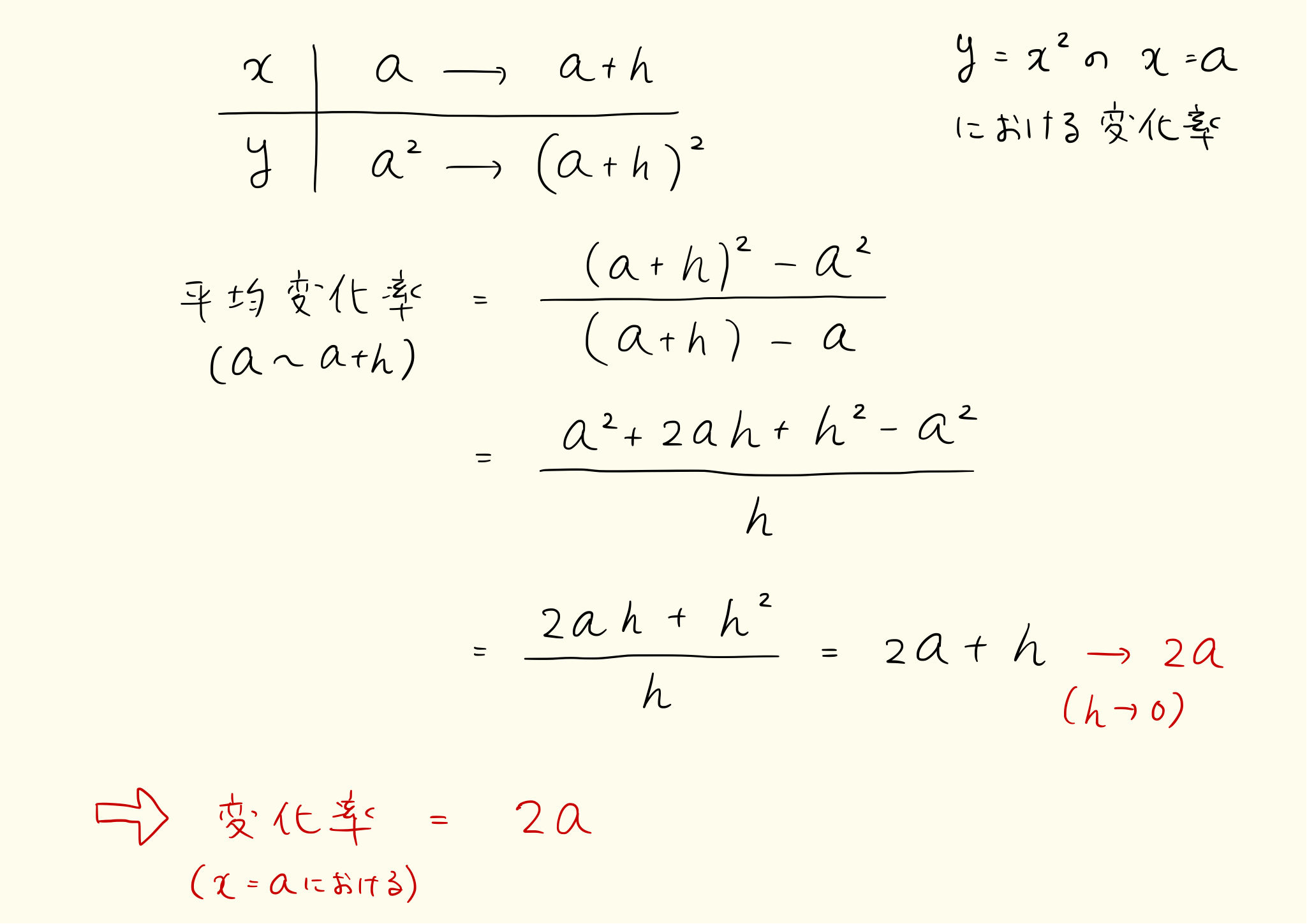
derivative_5
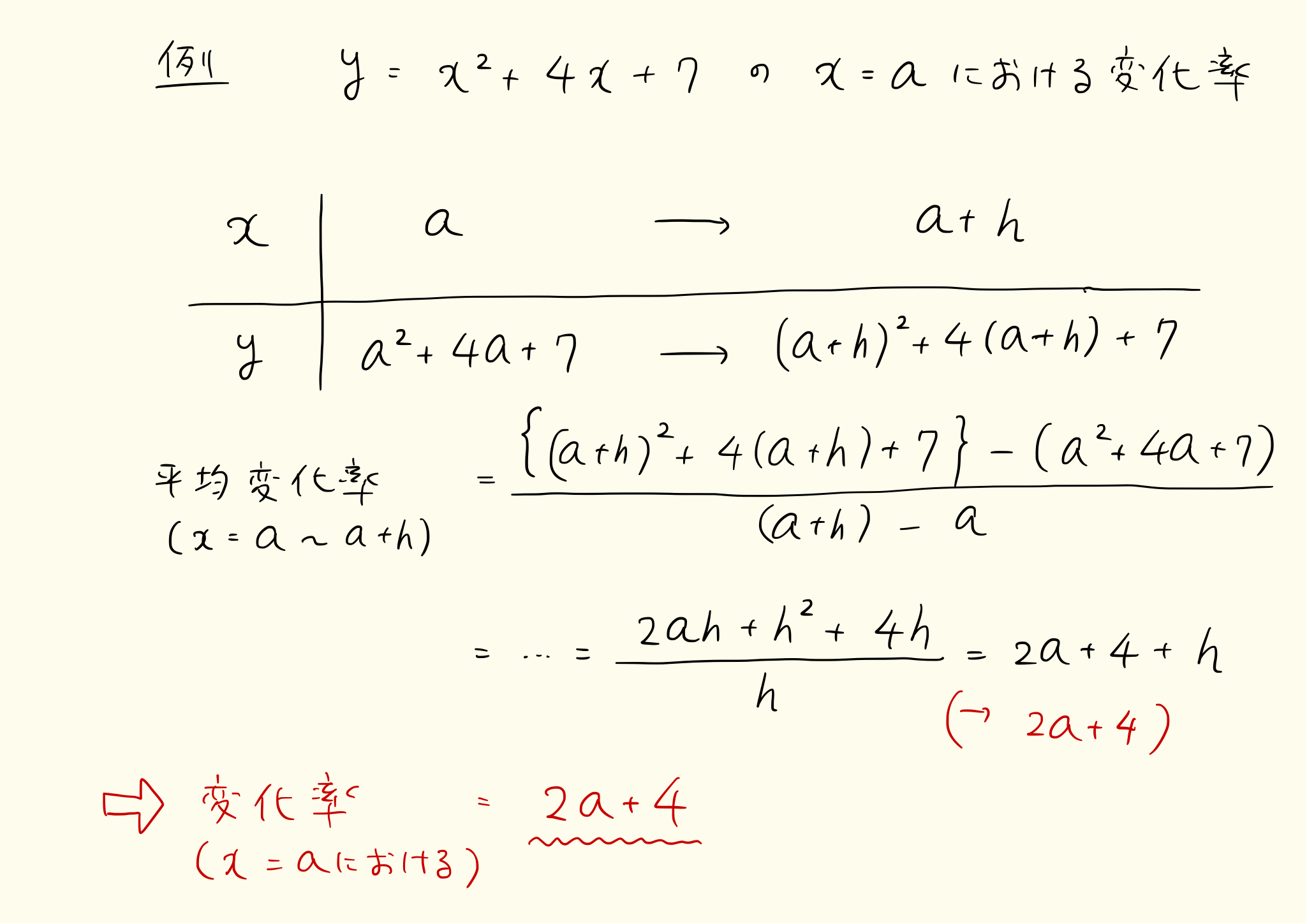
derivative_6
導関数

derivative_7

derivative_8
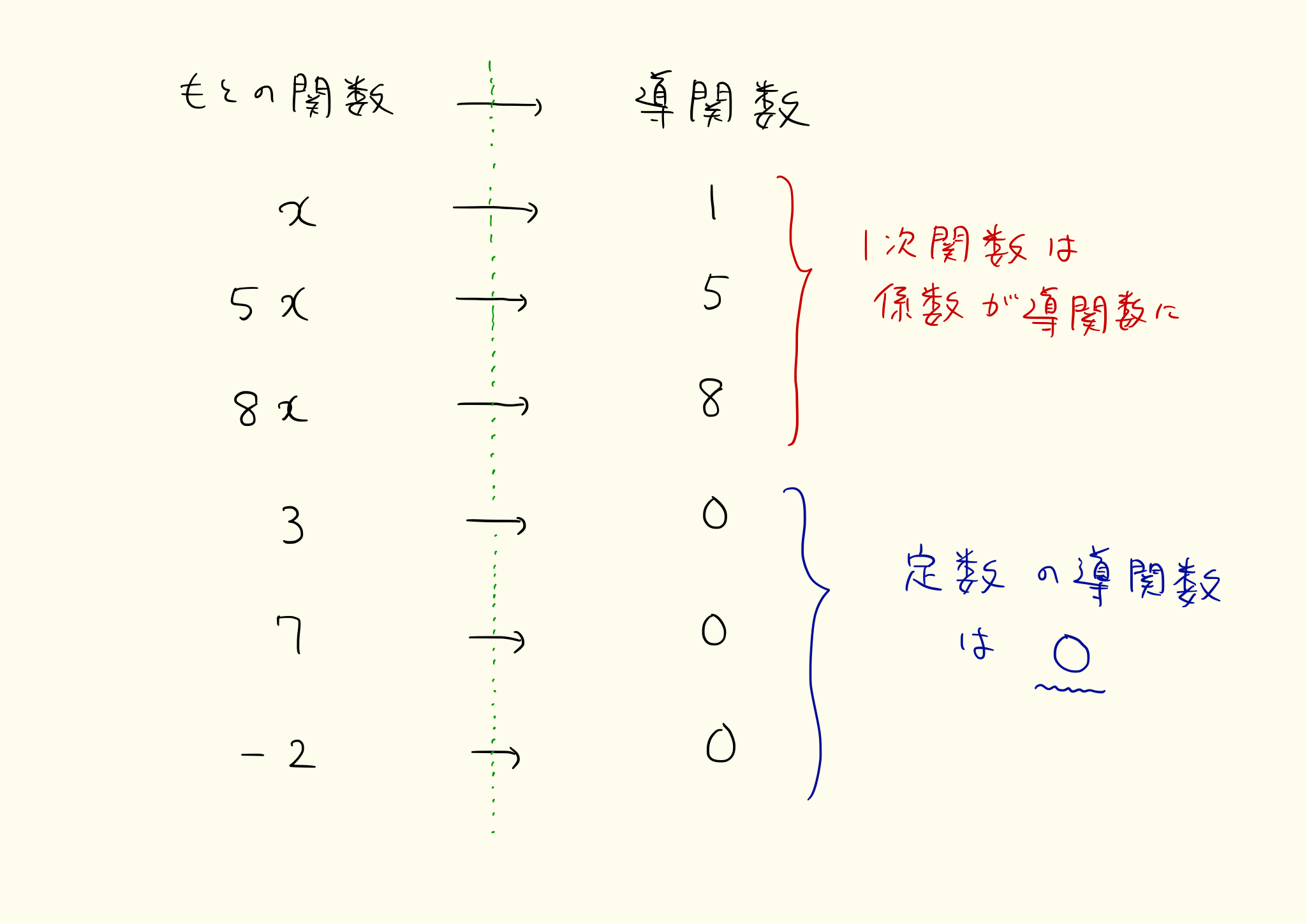
derivative_9

derivative_10

derivative_11
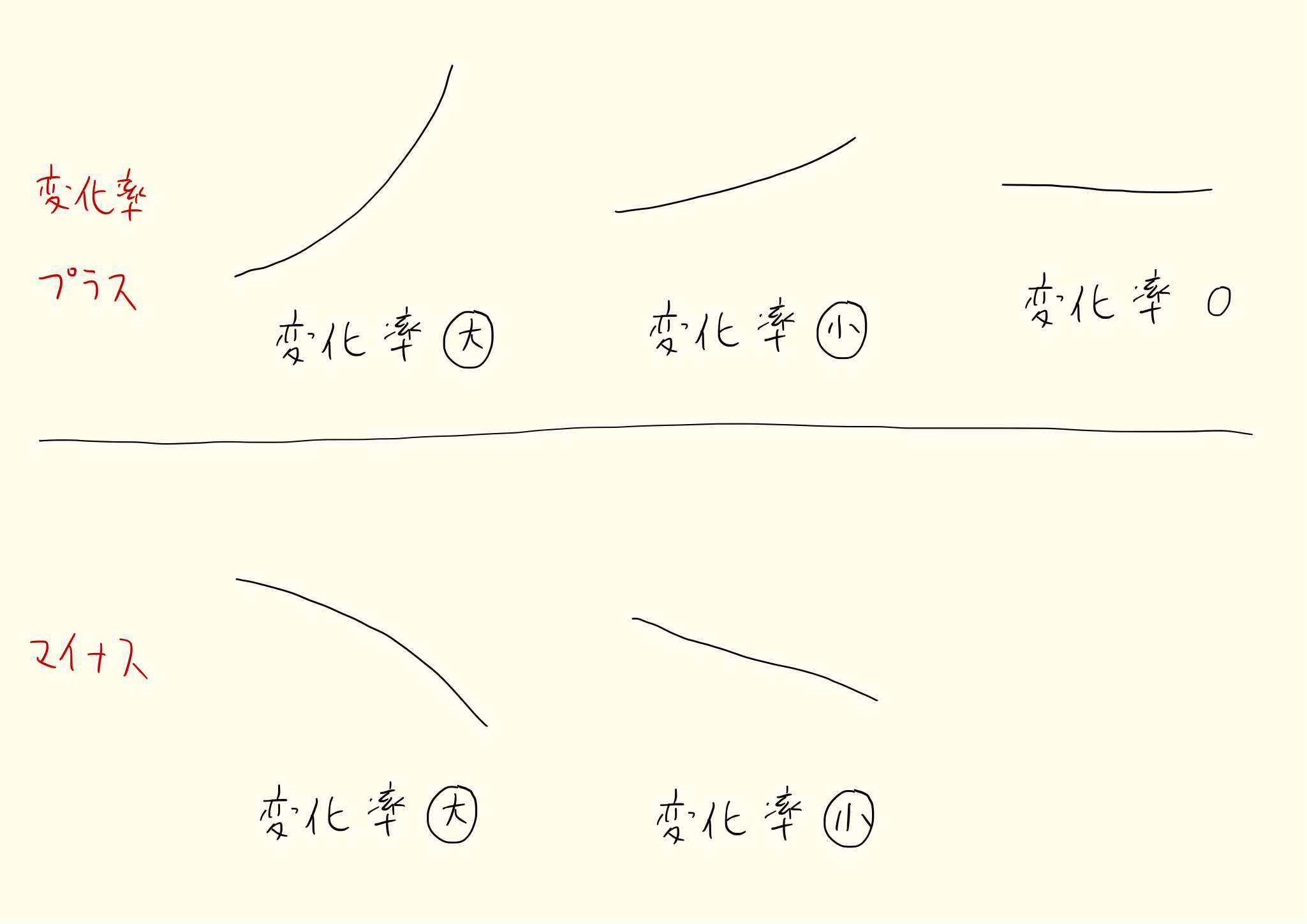
derivative_12









