数列は一定の値に収束するか、無限に発散するか、いつまでも不安定な値をとり続けるかの三パターンあります。特に三番目のパターンを振動といいます。

limit_1
一定の値に収束するとき、数列は収束します。例えば最初からずっと1の数列
1,1,1,…
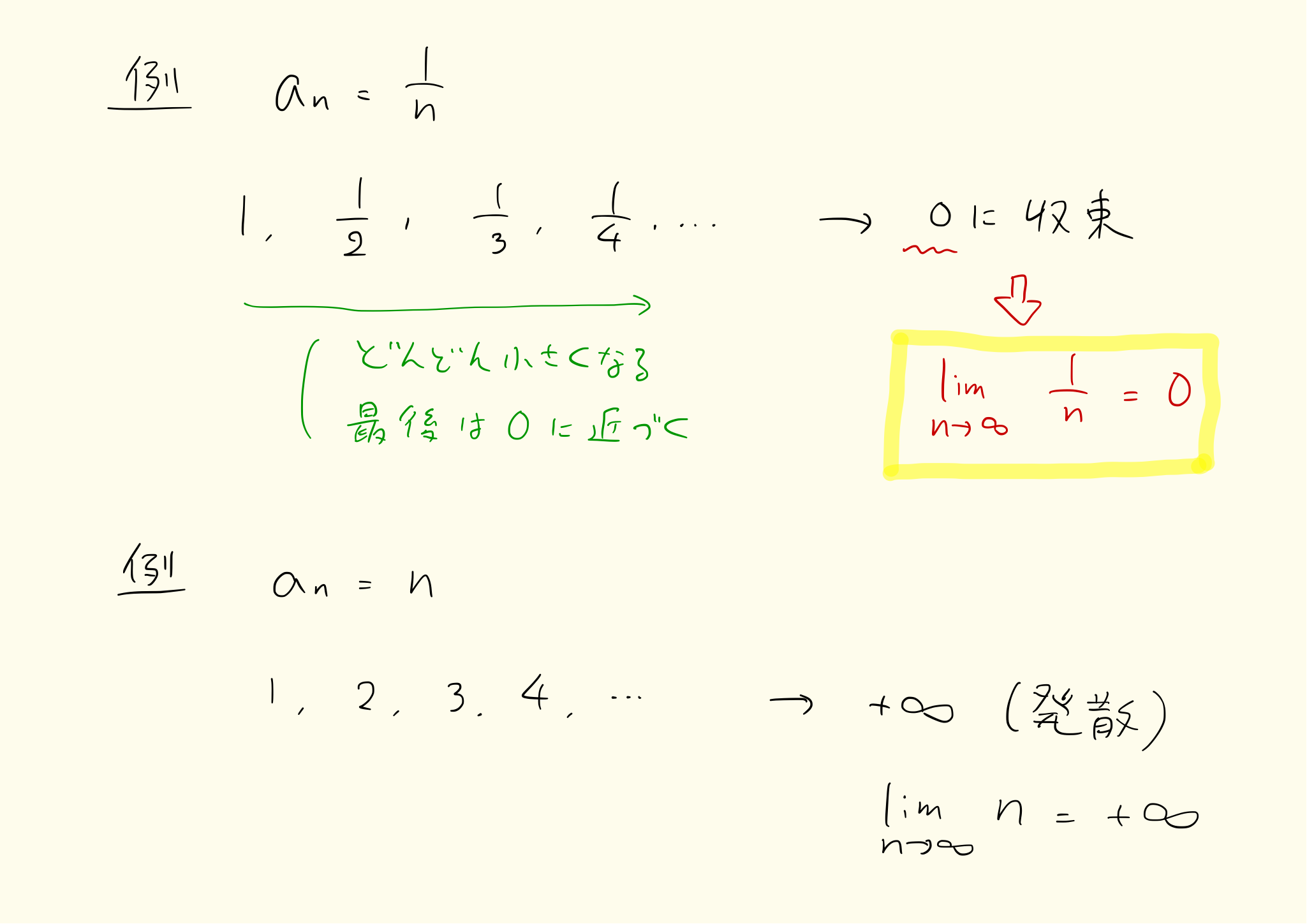
は1に収束します。1/nはnが大きくなるにつれて小さくなるため、最終的に0に近づきます。1/nは0に収束します。
limit_2
無限はプラスとマイナスの二パターンがあります。
公式
二つの数列について次の公式が成り立つ。
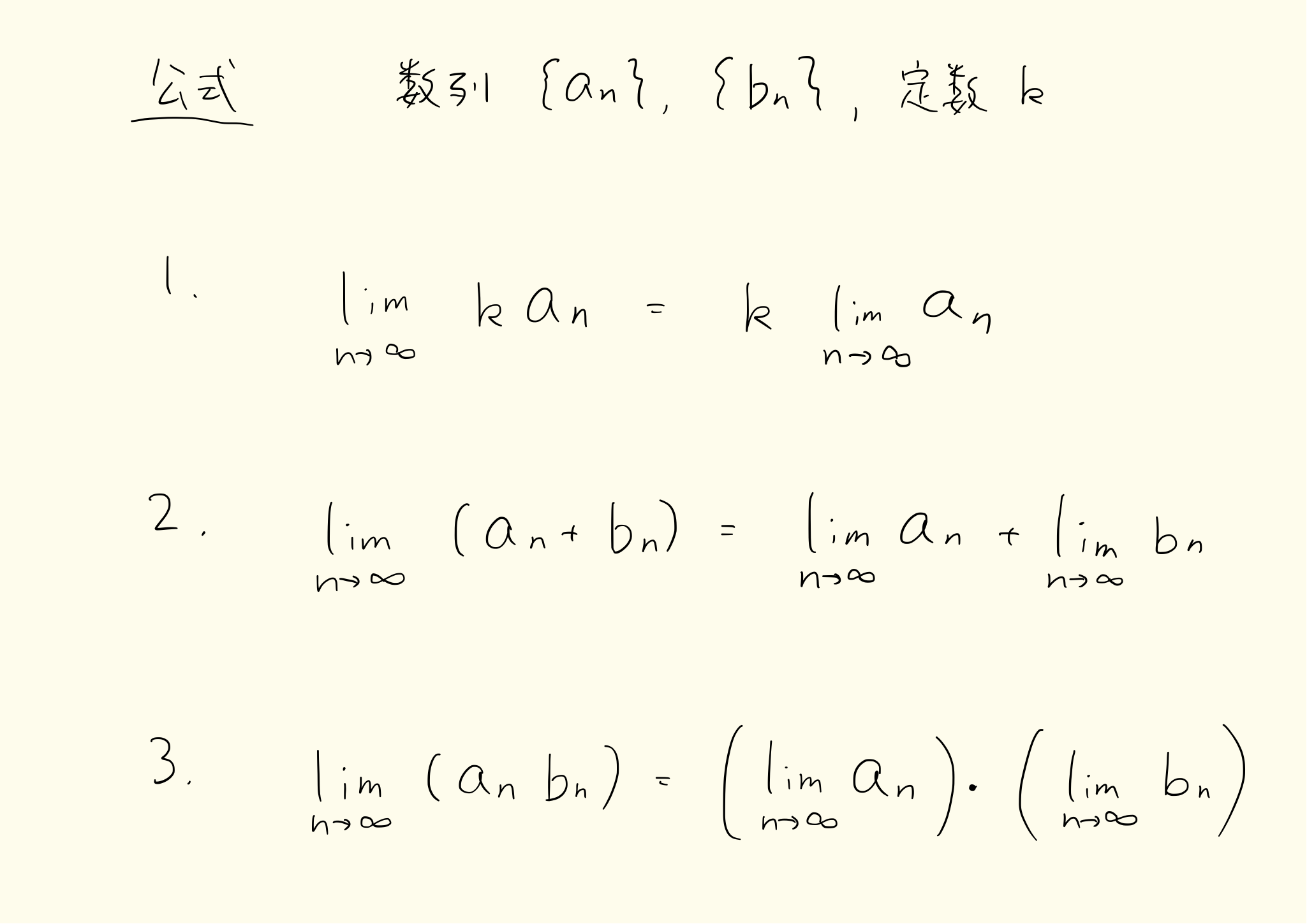
limit_3

limit_4
足し算やかけ算をしてから極限をとった値と、極限をとって足し算やかけ算をした値が一致します。この性質を使ってさまざまな数列の極限を求めることができます。
問題
極限の問題は1/nをつくることが基本です。数列の形が分数になっているタイプは、分母と分子をnなどで約分してn以上の項(n^2、n^3…)を消し、1/n以下の項(1/n、1/n^2、1/n^3…)をつくることで極限を求めます。
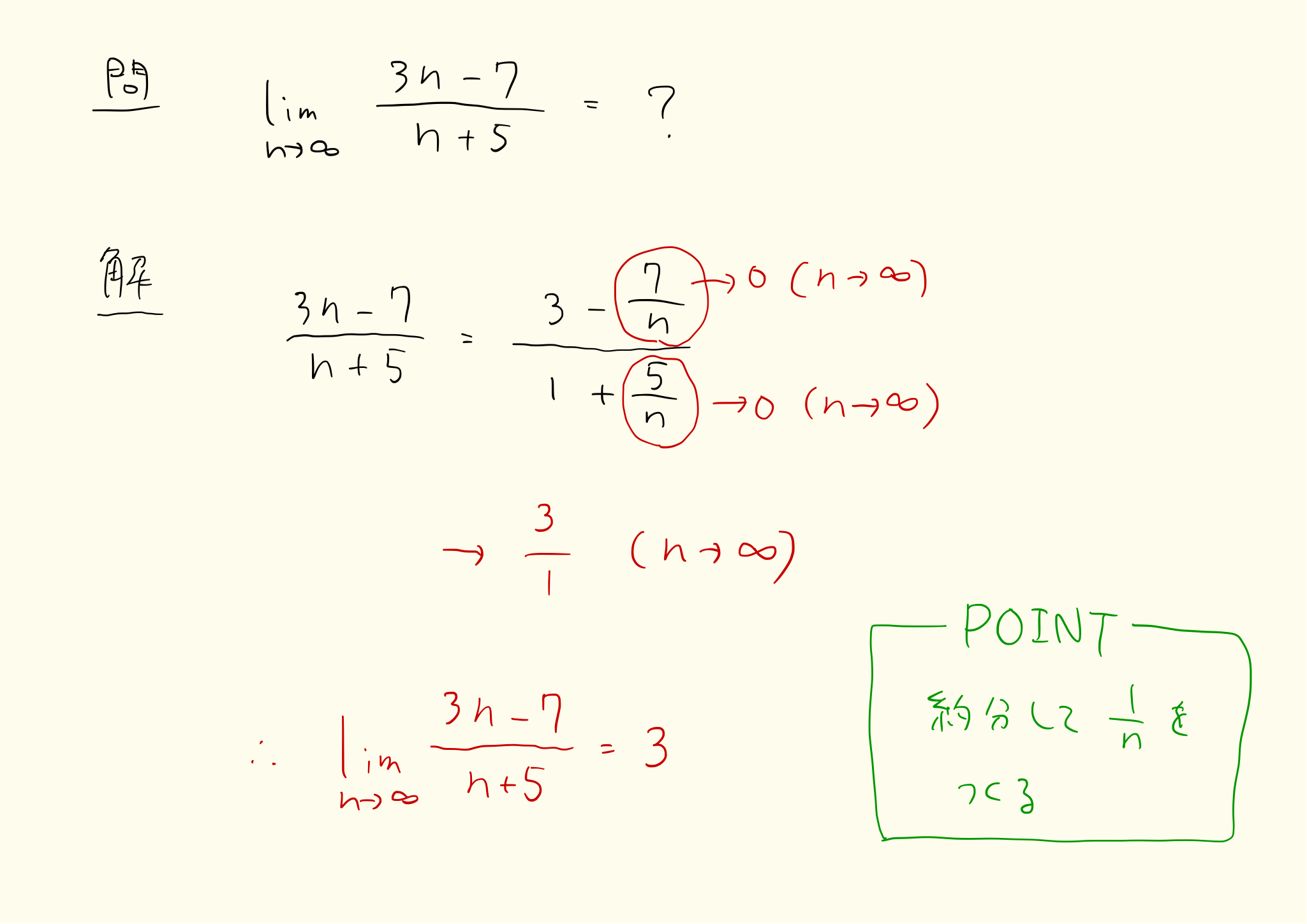
limit_5
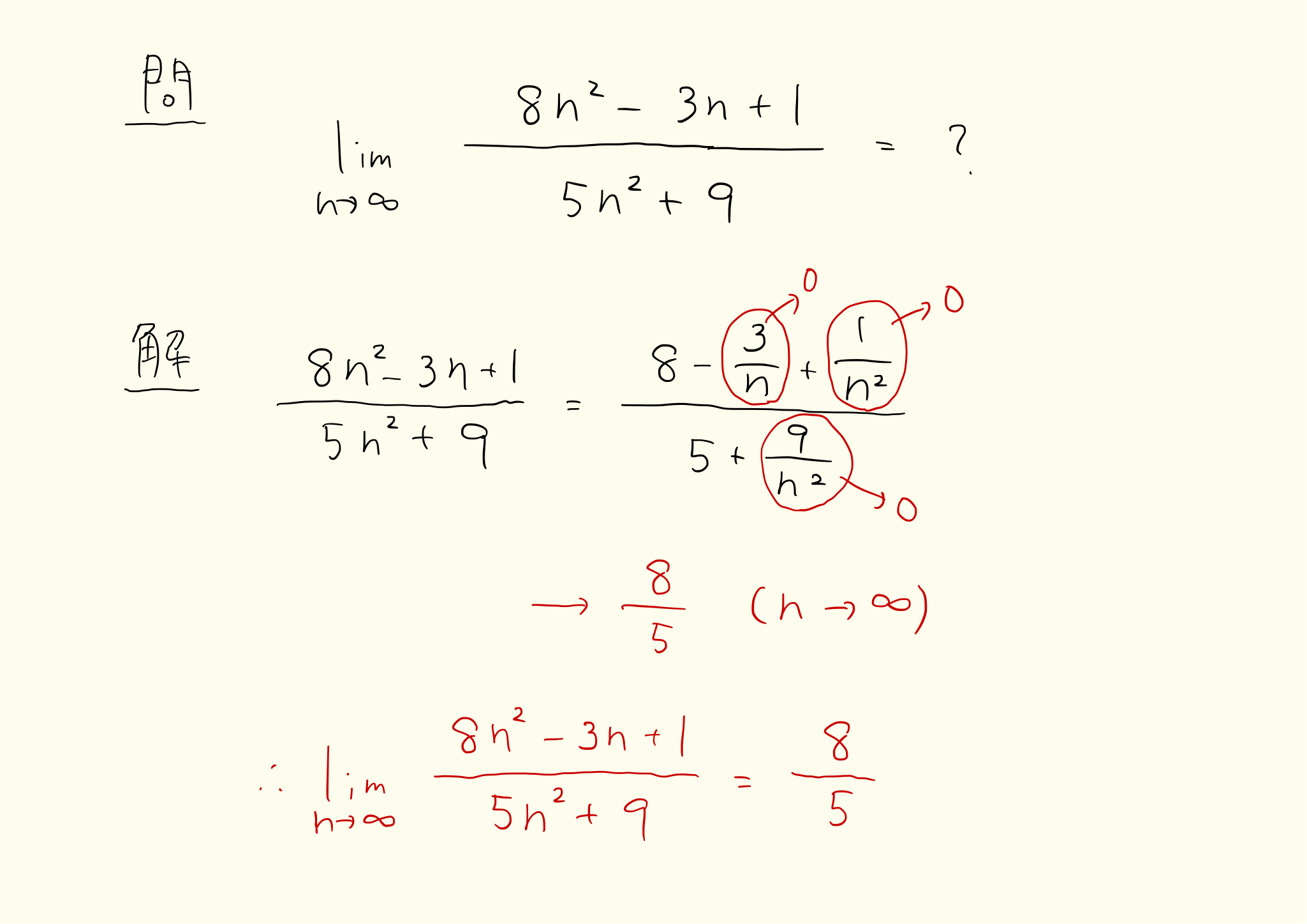
limit_6
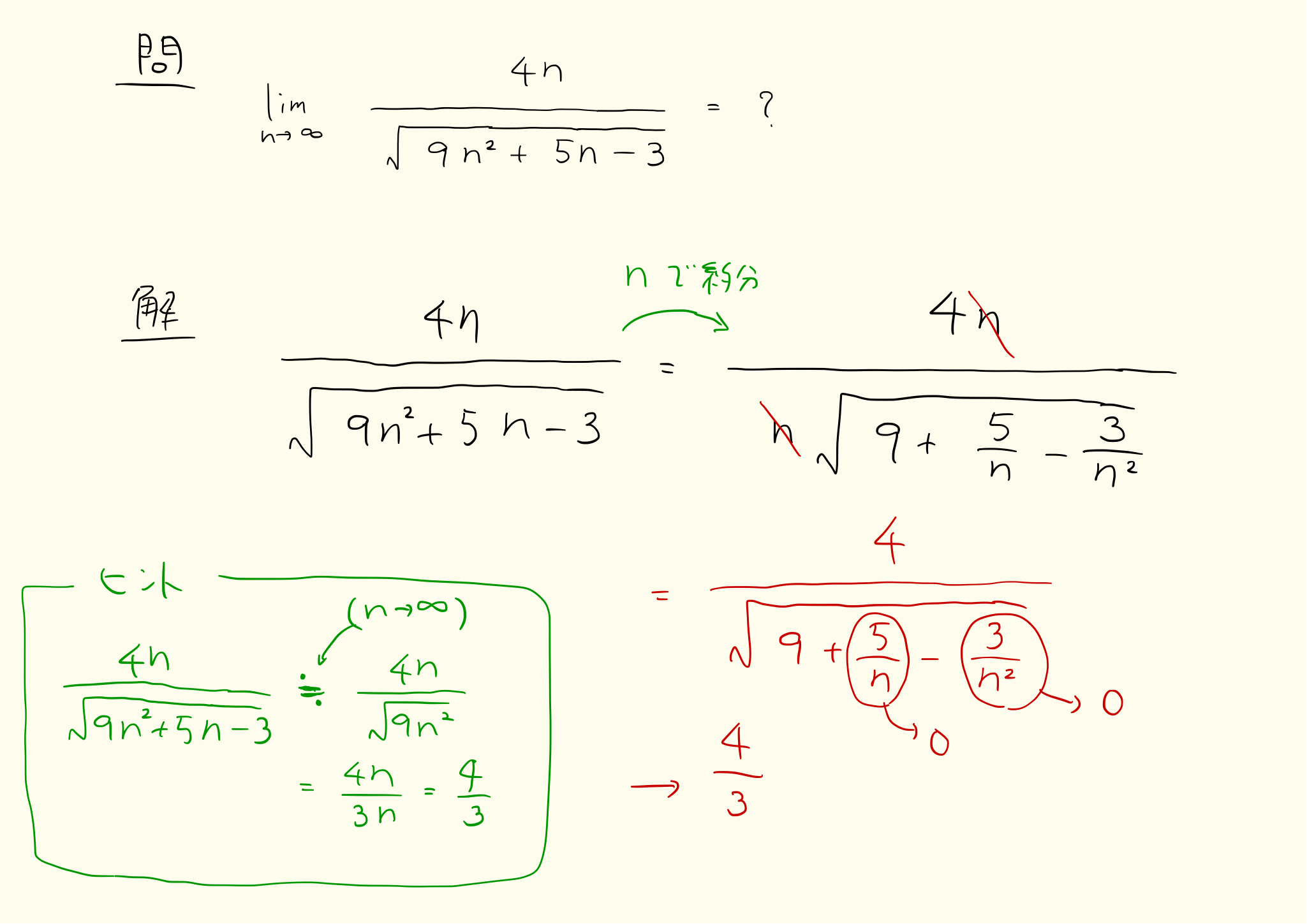
limit_7
問題は追加中…









