行と列の数が同じ行列は足したり引いたりできる。行列の足し算には交換法則や分配法則がなりたつ。行列と行列のかけ算も定義できるが交換法則はない。
2 次正方行列の足し算
行列の足し算は各成分をそのまま足してつくる。
もう一つ例を見てみよう。
引き算も同じ。
行列の引き算も成分を引くだけ。
行列のかけ算
行列のかけ算は実数と同じように の記号を省略する。行列のかけ算は前の行列の行と後の行列の列の内積を成分とする。
(1,1) 成分 = 前行列 1 行目 後行列 1 列目
(1,2) 成分 = 前行列 1 行目 後行列 2 列目
(2,1) 成分 = 前行列 2 行目 後行列 1 列目
(2,2) 成分 = 前行列 2 行目 後行列 2 列目
は内積のこと。
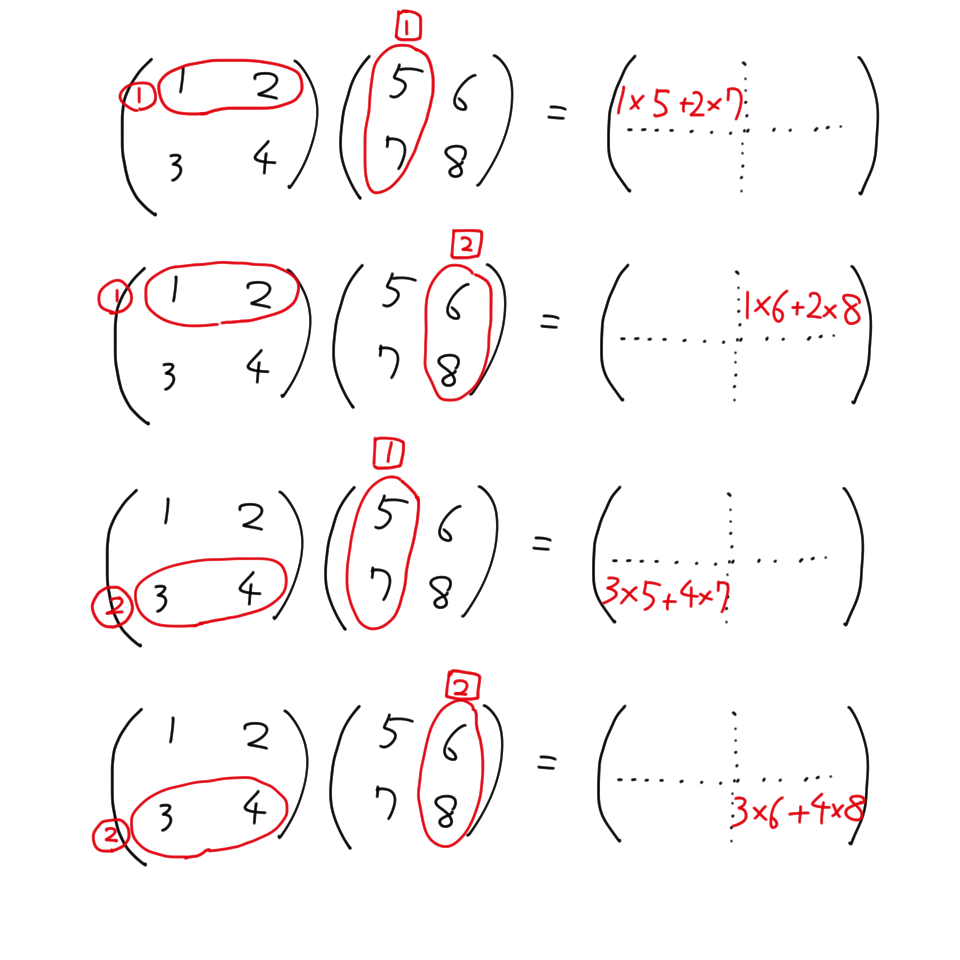
2matrix-multiplication
行列のかけ算は内積のくみあわせである。
行列のかけ算の確認問題
解答
行列のかけ算と単位行列
行列 を単位行列という。単位行列と任意の行列の積はその行列になる。
単位行列は実数の 1 と似ている。
行列のかけ算と逆行列
確認問題の最後の問題を見ると、違う行列をかけた積が単位行列になっている。
を の逆行列、または を の逆行列という。逆行列は実数の割り算や分数に近く、わかりやすく言うと
だが、線形代数ではマイナスのべき乗で逆行列を表現する。








