コンデンサーの極板は互いに互いを引きつける。これを極板間引力という。
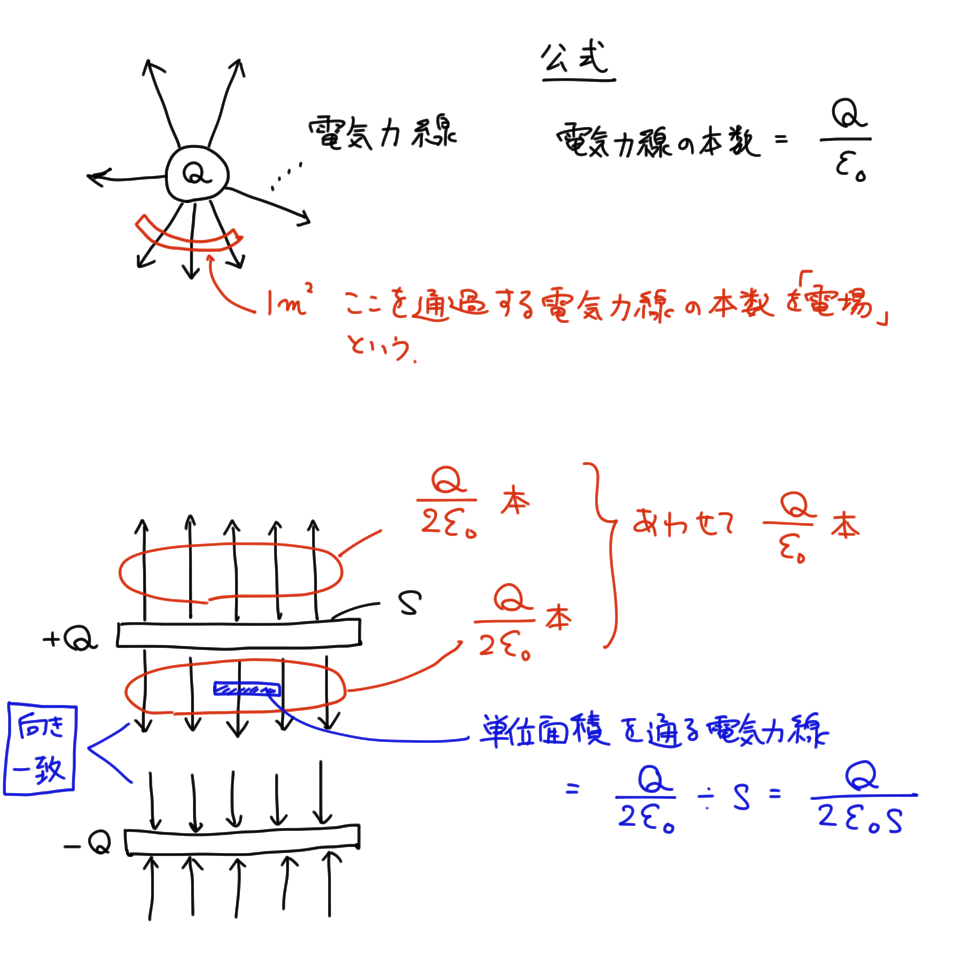
一枚の極板のつくる電場
ガウスの法則より電荷がつくる電気力線の本数は
である。 は真空中の誘電率。電場は単位面積あたりの電気力線だから、面積 の極板(一枚分)が作る電場は
となる。
極板間引力
極板間引力の定義
正の極板が作る電場も負の極板が作る電場も大きさは で、向きが一致する。
負の極板は正の極板がつくる電場 によって正の極板のほうに引きつけられる(静電気力)。これを極板間引力という。
同様に正の極板もまた負の極板がつくる電場 によって負の極板のほうに引きつけられる。
極板間引力の求め方
静電気力はその電荷(今は極板)と電場の積に等しい。
正の極板 は負の極板がつくる電場 によって
の引力を受ける。







