条件から関数を求める問題は、その関数を y = ax + b として a, b を求めます。
例題
グラフの傾きが 3 で、点 (2, 5) を通る一次関数を求めなさい。
解答
求める関数を y = ax + b とすると、グラフの傾きが 3 であるから
a = 3
となり、y = 3x + b となる。またこのグラフは (2, 5) を通るから
5 = 3・2 + b
3・2 + b = 5
6 + b = 5
b = 5 - 6 = -1
となり、求める関数は y = 3x - 1 となる。
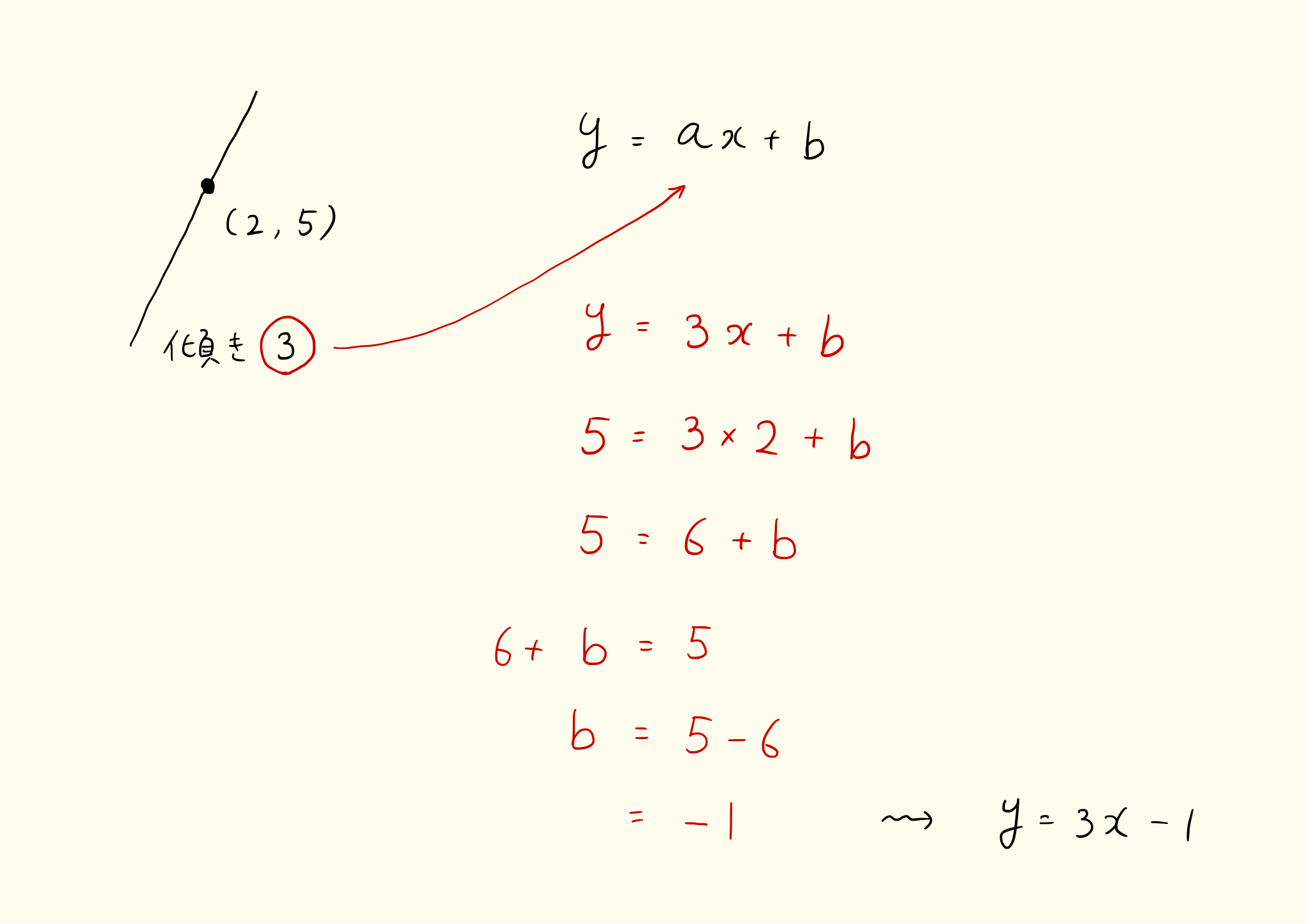
linear_function_gradient_point_1
問題
次の条件を満たす一次関数を求めなさい。
(1) グラフの傾きが 4 で、点 (-1, 3) を通る。
(2) グラフの傾きが -2 で、点 (5, -6) を通る。
(3) グラフの傾きが 0 で、点 (7, 9) を通る。
解答
(1)
求める関数を y = ax + b とすると、グラフの傾きが 4 であるから
a = 4
となり y = 4x + b となる。またこのグラフは (-1, 3) を通るから
3 = 4・(-1) + b
4・(-1) + b = 3
-4 + b = 3
b = 3 - (-4) = 7
となり y = 4x + 7 となる
(2)
求める関数を y = ax + b とすると、グラフの傾きが -2 であるから
a = -2
すなわち y = -2x + b となる。またこのグラフは (5, -6) を通るから
-6 = (-2)・5 + b
(-2)・5 + b = -6
-10 + b = -6
b = -6 - (-10) = 4
となる。
a = -2
b = 4
となり y = -2x + 4 とわかる。
(3)
求める関数を y = ax + b とすると、グラフの傾きが 0 であるから
a = 0
すなわち y = b となる。またこのグラフは (7, 9) を通るから
9 = b
となる。
a = 0
b = 9
以上から y = 9 となる。








