ド・モルガンの法則
を の部分集合とする。
この2つをド・モルガンの法則という。
が の部分集合であるとは に含まれるものがすべて にも含まれていること。
ド・モルガンの法則の例
とする( が の部分集合となっていることに注意。 に含まれるものがすべて にも含まれている)。
このとき
となり、公式の が成り立っていることがわかる。また
となり、公式の が成り立っていることがわかる。
ド・モルガンの法則とベン図
とする。図で表すと

de-morgan-u
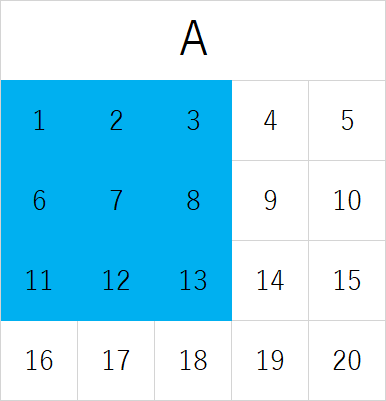
de-morgan-a
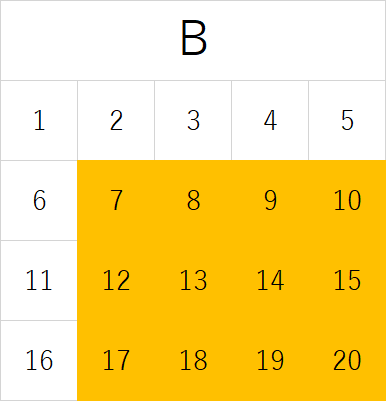
de-morgan-b
となる。
すると は以下のようになる。
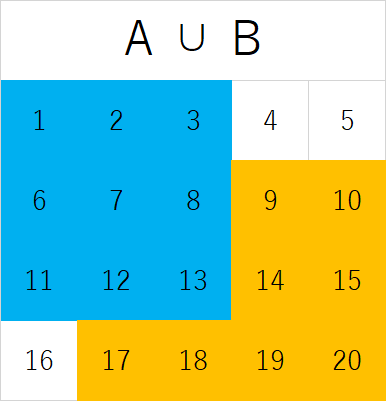
de-morgan-a-or-b

de-morgan-a-not

de-morgan-nota-and-notb
と の図がちょうど反転している。
これは の否定、つまり が に一致することを意味する。
2つの条件の否定(ド・モルガンの法則の応用)
ド・モルガンの法則の応用として2つの条件の否定に関する法則がある。
条件の否定の法則
を条件とする。
※ : 「または」、 : 「かつ」
例えば を は より大きく、 を は より小さいとしよう。すると
: は より大きく、かつ より小さい
: は 以下か、または 以上
: は 以下
: は 以上
: は 以下か、または 以上
となり、法則の が成り立っていることがわかる。








