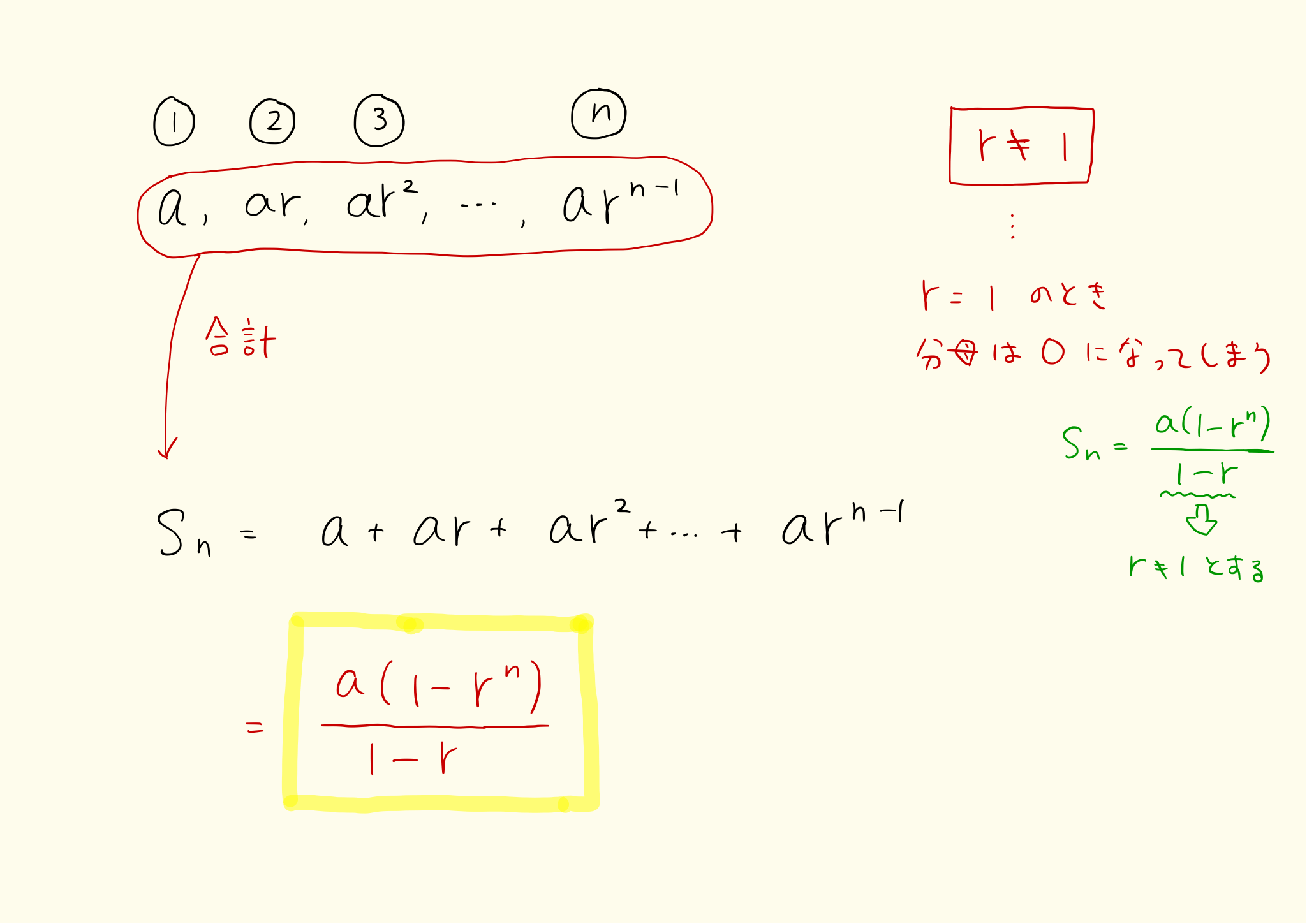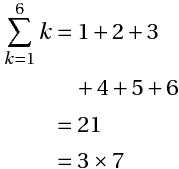数列（数学B）
15827
views
高校数学の数列で習う和の公式。公式を使った計算から、添字が1から始まってないシグマの難しい計算まで。
フィボナッチ数列では、隣り合う項の比が黄金比に収束する。漸化式はa_{n+2}=a_{n+1}+a_{n}となる。
漸化式の公式と解き方。a_{n+1}=pa_n+q, a_1=aの漸化式は a_n=(a-k)p^(n-1)+k となります…高...
漸化式は、数列の項どうしの関係を表した式です。 [882] 特殊な漸化式 [890] [889] [877] [876] 一般的...
等比数列とは、同じ数をかけてできる数列です。等差数列は同じ数を足していきますが、等比数列は同じ数をかけていきます。例えば \[ ...
フィボナッチ数列の $n$ 番目の項を計算します。通常のフィボナッチ数列は $1$ 番目と $2$ 番目の数を $1,\ 1$ ...
等差数列の例を見てみましょう。 $2,\ 5,\ 8,\ 11,\ \cdots,\ 95$ $2$ から $5$、$5$ から...
数列とは、ある規則に従って並んだ数の列のことである。 \[ a_1, a_2, a_3, \ldots, a_n, \ldots...
数列 $\{a_n\}$ に対して、隣り合う項の差 \[ b_n = a_{n+1} - a_n \] で定まる数列 $\{b_...
各項の逆数が等差数列をなす数列を調和数列という。 数列 $a_1, a_2, a_3, \ldots$ が調和数列であるとは、 ...
$\displaystyle\sum_{k=1}^{n} a_k$ は $a_1 + a_2 + \cdots + a_n$ を...
分数の形をした数列の和を求めるとき、部分分数分解が有効な場合がある。分解後に隣り合う項が打ち消し合い（telescoping）、...
数列をいくつかの組（群）に分けて考える問題を群数列という。 たとえば、$1 | 2, 3 | 4, 5, 6 | 7, 8, 9...
漸化式 $a_{n+1} = pa_n + q$（$p \neq 1$, $q \neq 0$）は、特性方程式を使って解ける。 ...
漸化式 $a_{n+1} = a_n + f(n)$ の形を階差型という。$f(n)$ は $n$ の関数である。 解法 $a_...
$a_{n+1} = \dfrac{a_n}{pa_n + q}$ のような分数型漸化式は、逆数をとることで解ける場合が多い。 ...
三項間漸化式 $a_{n+2} + pa_{n+1} + qa_n = 0$ は、特性方程式を使って解く。 特性方程式 $x^2...
2つの数列が互いに絡み合った漸化式を連立漸化式という。 \[ \begin{cases} a_{n+1} = pa_n + qb...
数学的帰納法は、自然数 $n$ に関する命題を証明するための方法である。 証明の手順 命題「すべての自然数 $n$ について $...
数学的帰納法のさまざまな応用例を見ていく。 例題1：不等式の証明 $n \geq 1$ のとき $2^n > n$ を証明せよ。...
無限等比級数とは、等比数列の無限個の項の和である。 \[ \sum_{n=1}^{\infty} ar^{n-1} = a + ...
無限級数 $\displaystyle\sum_{n=1}^{\infty} a_n = a_1 + a_2 + a_3 + \...
