二項分布 とは、確率変数 について における確率 が で表されるような確率分布。ここで 。
確率変数 が二項分布 にしたがうとき、確率変数 の期待値、分散、標準偏差は次のようになる。
期待値
分散
標準偏差
二項分布は「ある行為をくりかえす」ような問題で出る。
参考
分散と標準偏差の求め方
二項分布になる確率変数の例
コインを投げて表になる数をカウントするという問題を考える。ここでは3回投げることにして、確率変数と確率分布の基本を参考にする。
表の枚数が 枚 …
表の枚数が 枚 …
表の枚数が 枚 …
表の枚数が 枚 …
表の出る枚数が二項分布の定義に沿っていることがわかります。この場合、 となる。
3枚のコインを投げたときの表の出る枚数の確率分布から二項分布の諸公式を確かめる
であることに注意。
\begin{eqnarray} E(X) & = & 0 \cdot \frac{1}{8} + \cdots + 3 \cdot \frac{1}{8} = \frac{3}{2} \\ & = & 3 \cdot \frac{1}{2} \\ & = & np \end{eqnarray}
\begin{eqnarray} V(X) & = & E(X^2) - {E(X)}^2 \\ & = & 0^2 \cdot \frac{1}{8} + \cdots + 3^2 \cdot \frac{1}{8} - \left(\frac{3}{2}\right)^2 \\ & = & \frac{24}{8} - \frac{9}{4} = \frac{3}{4} \\ & = & 3 \cdot \frac{1}{2} \cdot \frac{1}{2} \\ & = & np(1-p) \end{eqnarray}
\begin{eqnarray} \sigma(X) & = & \sqrt{\frac{3}{4}} \\ & = & \sqrt{3} \cdot \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2}} \\ & = & \sqrt{np(1-p)} \end{eqnarray}
となり、二項分布の公式が成り立つ。
エクセル(Excel)を使った二項分布の確率計算
エクセルのBINOMDISTを使うと二項分布の確率が簡単に計算できる。
BINOMDIST(成功回数,試行回数,成功率,論理)
例えば「コインを 回投げて 回表が出る確率(表が出る確率を とする)」は
BINOMDIST(3,20,0.5,false)
とする。表が出る確率が であれば、三番目の引数を から にする。
コインを 回投げて 回表が出る確率は下のようになる。なお確率論では成功回数を生起回数と呼ぶことがある。
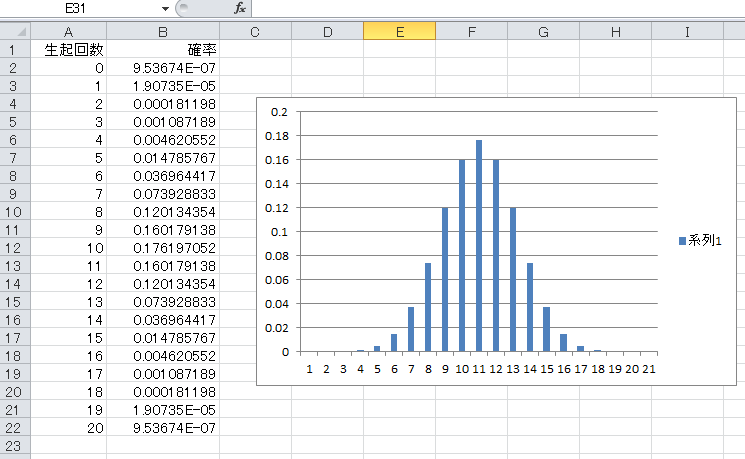
binomial
エクセル(Excel)の確率計算例
コインを 回投げて 回表が出る確率(表が出る確率を とする)
| 生起回数 | 確率 |
|---|---|
| 0 | 0.000976563 |
| 1 | 0.009765625 |
| 2 | 0.043945313 |
| 3 | 0.1171875 |
| 4 | 0.205078125 |
| 5 | 0.24609375 |
| 6 | 0.205078125 |
| 7 | 0.1171875 |
| 8 | 0.043945313 |
| 9 | 0.009765625 |
| 10 | 0.000976563 |
コインを 回投げて 回表が出る確率(表が出る確率を とする)
| 生起回数 | 確率 |
|---|---|
| 0 | 9.53674E-07 |
| 1 | 1.90735E-05 |
| 2 | 0.000181198 |
| 3 | 0.001087189 |
| 4 | 0.004620552 |
| 5 | 0.014785767 |
| 6 | 0.036964417 |
| 7 | 0.073928833 |
| 8 | 0.120134354 |
| 9 | 0.160179138 |
| 10 | 0.176197052 |
| 11 | 0.160179138 |
| 12 | 0.120134354 |
| 13 | 0.073928833 |
| 14 | 0.036964417 |
| 15 | 0.014785767 |
| 16 | 0.004620552 |
| 17 | 0.001087189 |
| 18 | 0.000181198 |
| 19 | 1.90735E-05 |
| 20 | 9.53674E-07 |








