接線の傾きがわかると法線の方程式もわかります.法線の方程式を求めるときは
- 導関数
- その点における微分係数
- 法線の方程式
の順番に計算します.接線と法線は垂直に交わる線で,その傾きの積は です.例えばある点における接線の傾きが のとき,その点における法線の傾きは
となります.
例題
の導関数は だから, における微分係数は
で,接線の傾きは とわかります.接線と法線の傾きは積が になるため,法線の傾きは
となり,法線の方程式は
\begin{align}
y &= (-1)(x - 2) - 6 \
&= -x - 4
\end{align*}
となります.
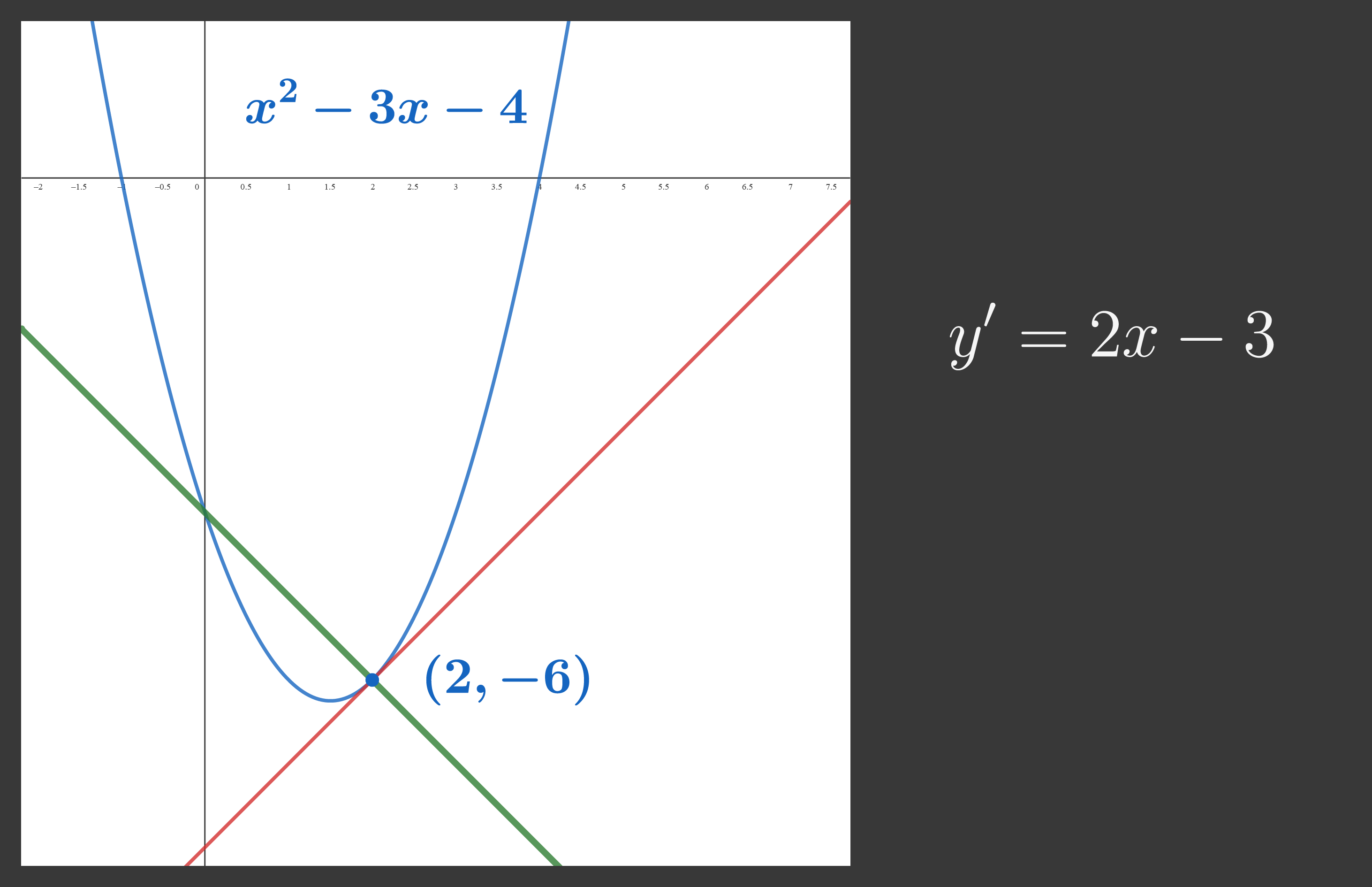
二次関数の法線








